Become the Subject

My Speech is now live on youtube! For those of you who missed me talking at MfA’s MT-squared, here it is: Become the Subject.

The script for my speech is below (since this video is uncaptioned):

Good evening. I’m delighted to talk with you tonight. First, let me share a dirty little secret: math class is not as fun as science class! Controversial, I know. I realized this as a first-year teacher when I taught both. The problem is I’m a math teacher, and passionate about it!

 

Those of you who are science teachers likely enjoy designing classroom experiments that facilitate discussions by unpacking student observations. I remember one such experiment, my first-year teaching, when I put food coloring in cups of cold and hot water.   My 6th graders watched, fascinated, as the color spread much more quickly in the hot water. In an animated discussion, we made connections to brewing tea in hot water, and ultimately spoke about the impact of temperature on the speed of molecules. My students were excited and talked enthusiastically about the experiment.

 

Later that day, I taught those same students a math lesson. They showed much less interest in adding fractions with unlike denominators. Class became a battle: I spent all my energy trying to get students to do the math, while they spent all their energy trying to distract me and avoid doing math. “What are you doing this weekend, Mr. G?” they asked. “Do you have a girlfriend?” “Do you have any kids?” When asked a personal question, I stonewalled with, “That’s off topic” or “That’s irrelevant.” I thought I was keeping them on task. But what I didn’t realize was that some students were genuinely curious about who I was and wanted to connect with me, and I was rebuffing their efforts!

 

This leads me to the challenge we face: “How do we provide students with classroom experiences that promote rich discussions and engage their curiosity in math class?” My principal advised, “Just make your lessons more engaging.” “But how?” I asked. I hadn’t learned how to do that in grad school! Meanwhile, my students seemed overly curious about me and uninterested in the math. Then, during my second year of teaching, I had an epiphany and realized that I could use one problem to solve the other!

 

The breakthrough came after I had delivered a boring lesson on converting Celsius to Fahrenheit. My coach observed that while my students were plugging numbers into the formulas, they had no motivation—it was sheer drudgery. She suggested an alternative: What if I had launched the day’s lesson with a story? Suppose I said I’d gone to Canada, checked the weather before going outdoors and it was 20 degrees. I bundled up tight, expecting it to be bitterly cold, but when I got outside, I was sweating. What do you think happened? This would pique my students’ interest and elicit from them that I’d interpreted a temperature in Celsius as Fahrenheit. Now we had a REASON to learn how to convert temperatures – so we wouldn’t make the same mistake Mr. G made on his Canadian trip.

 

Using storytelling to hook students and help them learn math was a brand-new idea for me. Immediately, I found it highly effective. The first time I tried this, the kids were more attentive and enthusiastic than I had ever seen them. And so, I became a storytelling teacher. The purpose of my stories wasn’t to tell the literal truth about my experiences, but to cultivate rapport with my students and develop a reason for the mathematics. I leveraged student curiosity about me to engage them before they even realized we were solving math problems. Gradually, I evolved from fabricating stories to turning actual incidents in my life into math problems.

 

For example, last year, I launched a problem in class like this. “How many of you like bagels? [Encourage audience to raise their hands]. Me too! I love bagels. We’re lucky we live in NYC, because we have the world’s best bagels. Sadly, my Bubbe doesn’t live in NYC; she lives in Connecticut, where they don’t have great bagels. So like any good grandson, I brought her New York bagels whenever I visited. One time I had to visit on a Monday, when my local bagel store is closed, so I couldn’t bring her any bagels! Let me tell you, my Bubbe never let me hear the end of that! Every subsequent visit, she would ask, “Did you bring the bagels this time?” “Can you believe he forgot the bagels?” So to make sure it would never happen again, I did a little bit of research and I found two other good bagel stores in my neighborhood: Bob’s Bagels and Tom’s Bagels. And both are open on Monday! Can you all help me figure out where I would get the better deal on bagels for my Bubbe?”

 

My students really got on board with this problem. As I monitored student discussion, I heard lots of conversations about their favorite bagel stores. Students analyzed each other’s methods of determining which store offered the better deal. They were seeing for themselves how mathematics is a powerful tool to solve problems in daily life.

 

At the end of the year, I asked my students to write a letter with any advice on how to be a better teacher and how they would like me to remember them. One student wrote, “Now, as for any advice, I liked how you would often turn your stories into math problems, it makes math more fun… I want you to remember me as… ‘the kid who reminded you that you forgot to bring your grandma bagels that one time.’” Thanks, kid! That story had stuck with him through subsequent units, and he recalled it as THE thing he wanted me to remember about him. Clearly, my stories resonated with him. 

 

In building relationships with my students, I’m drawing on what I know about relationships in general. In psychotherapy, there is a term for using yourself to create empathy and a relationship with your patients: a therapeutic use of self. I propose that teaching needs to coin its own term: a pedagogical use of self. A pedagogical use of self is when you strategically embed yourself into the curriculum in stories that will captivate students and cultivate a community of mathematicians—or scientists—in your classroom. Such sharing about yourself will strengthen your relationships with your students. Your curriculum will come to life, your students will get to know you and you’ll draw them into your subject matter.

 

By using my life pedagogically, I model what mathematics can do for anyone and show students how math can be a tool to help us make sense of, explain, and evaluate our own lives. In eight years of teaching, I’ve evolved from following the lie “Don’t smile until Christmas” and worrying about staying on task, to spending the whole first day of school getting to know who my students are and introducing myself to them – everything from the dog I have to the absurd number of board games I own. By sharing my truths with the students, I build trust and inspire them to share their own truths with me. As a result, I am currently experiencing powerful, vibrant relationships with students and enjoying seeing some of them develop a passion for math. 

 

I hope my evolution will inspire you to embrace a pedagogical use of self as a valuable tool in your own classrooms. Ask yourself, “What are your Bubbe’s bagels stories?” Thank you.

Honoring #MLK with Action from Anger

Last week, I tweeted about one of the two restorative circles I ran in my two math classes that weren’t functioning well. I haven’t tweeted about the second class because there’s been more on my mind about it, and I haven’t been able to put it all into words. However, in honor of MLK day and several of his quotes, I want to share something that happened in my last period class during our circle on Thursday (and then my follow-up after school & on Friday/this weekend).

I started with the four agreements from courageous conversations about race:

1. Stay Engaged
2. Experience Discomfort
3. Speak from Your Truths
4. Expect and Accept non-closure (still open).

I explained what each of those meant in kid-friendly terms and expressly said we weren’t “naming names,” but speaking about how WE felt during class. Then I asked the same opening question, “How does math class feel to you right now?” and I listened to the students. Because this was last period and their issues are different than my other class, the conversation went very differently. I had three students talk about DREADING school & many kids who spoke about feeling bored, burnt out or ready to go home from school at the end of the day. I asked them about what they found engaging in their lives and what would help keep their attention on math at the end of the day as our two follow up questions (different from the morning’s class who was having trouble with calling out and interrupting people making mistakes, who I asked how it feels when they make a mistake in math class & who they ask for advice). I heard the students of last period request more games, physical activity, and hands-on activities, as well as stories that were more “fun and deep,” so my Friday lesson attempted to incorporate several of those aspects to be more engaging for them. While it was obviously just a start, many students who were there expressed that it did feel different and fun and nice (some of the students who said they dread school had not come to school on Friday, supposedly fearing a math test – but that’s for another post).

There was one student in that last period class who spoke up whose contributions were very different. She mentioned that students had been laughing at her because I call her by a different name than the other teachers do, but that in her culture, it’s traditional for people to get two names, not just one, and so the second name I was calling her was actually part of her name and not just a nickname I had made up for her (which was what other students insinuated). But most teachers just read off the roster what your name is, and they don’t ask you what you want to be called, so the other teachers just called her by the first part of her name. She said she was sick of being teased and harassed about the name that I called her because other kids didn’t understand.  Names and naming have been on my mind a lot lately, in part because of my own experiences with names, realizing I was mispronouncing a white student’s name earlier this year, and another student for most of last year. Plus, Dulce-Marie Flecha had just posted about pronouncing her name correctly on twitter (Duel-seh-Marie, for those who don’t know), so I was thinking about the importance of student names already.

I spoke with my student after class a bit more about it, and she expressed that she had students who were in 7th and 8th grade that she didn’t even know teasing her in the hallway, and I felt angry. I began writing an email to my colleagues to call her by both names, but I decided to stop by the 6th grade AP’s office, since I had just seen he was in. I told him a bit about what had happened, and he expressed that he thought it would be a better message coming from guidance, and that I should refer the situation to our guidance counselor. I told him I didn’t understand why, since I was the person this student had felt comfortable sharing this with, and that it felt like passing the buck to pass off the issue to the guidance department – and also, I didn’t understand why teachers would be more receptive to hearing this information from the guidance counselor and not from me, one of their colleagues.

The other piece that felt uncomfortable throughout the conversation was the fact that he suggested we talk to her parents and find out what name they wanted us to call her. I expressed the fact that it shouldn’t be necessary to ask parents – especially in the case of a trans student, that would be violating their right to privacy and self-determination (NYC protects a student’s right to be called ANY name THEY use and identify with, and doesn’t require parental notification of such, especially if it would potentially harm the kid). He pushed back & said that for all of the other students whose names differed from the names on their records, the request to use an alternate name came from the parents. I said that it didn’t have to and shouldn’t have to, that we should be asking the students about names and pronouns and not making assumptions.  He expressed that she had never told any other teacher about this name difference, and I challenged “Which other teachers asked?” & he said something about her being capable of self-advocating. I said maybe, but why should she have to. I also expressed that not every parent felt comfortable or spoke English fluently enough to make these kinds of demands of the school, & he said he’d spoken to her parents about other (disciplinary-related) things and they were fluent in English and seemed capable of asking for that if they had wanted her to be called a different name. Our conversation didn’t seem to be moving forward, and he was distracted (and continually shutting down my attempts at engaging with “I still stand by what I said…”). I left with this unresolved, but continuing to chew on what he had told me.

He thought about it for a bit, and came to find me in my classroom a bit later to continue the conversation. I appreciated the fact that he acknowledged the conversation was unresolved, that he wasn’t feeling well and hadn’t been giving me his full attention, but now he could give the conversation more attention (though he was still feeling ill). We continued talking about the two issues. He mentioned the idea that people might be more receptive to hearing critical feedback from someone who didn’t seem like a “peer” but seemed like an outsider (i.e. guidance) because it would feel more accusatory coming from me. I expressed that I felt angry, like we had robbed this student of her name.

He also mentioned a fact that infuriated me (though I don’t remember now whether it was during the first part of our conversation or the second part). My school population is about 50% Hispanic students and has been for all of its 6-year history. This was NOT the first example he could think of a student who used two names at home that our school hadn’t “caught” initially, and that eventually (perhaps by 8th grade, where our curriculum focuses on self-advocacy) most students who wanted to go by a name different than the one on the register ultimately asked the school to do so (that he KNEW of! was the piece I thought but didn’t articulate at the time).

I pushed back on this assumption, and tried to make an analogy to my experiences in college using Kit, a name different from my legal name at the time (and even in K – 12 school, I never used my legal birth name, always a nickname). I expressed how every year, at the start of class, I had to tell my teachers to use a different name than on the register for me because I didn’t use that name. He expressed something like, “You should be proud of yourself for advocating for yourself like that!” and I snapped back, “No, I didn’t want to have to ask for that. It’s exhausting to constantly have to fight that battle. I wanted the teachers to ask me what name and what pronouns to use, and not just me – but to ask EVERYONE, so I didn’t stand out as different.” He tried to make a connection with the 8th grade curriculum teaching our students to advocate for themselves, and I said, “But that’s ridiculous. Not everyone is going to stand up to a teacher and tell them to do something different. We’re the adults; we’re the ones in power. And we have the power to change the system so that the names we use for students are the names they identify with. We shouldn’t be changing their names or making them ask us.”

He seemed to chew on this idea a bit, and said next year, things could be different, and we could discuss how at some of our Wednesday 6th grade meetings. He reiterated how he thought that the guidance department would be better suited to introduce this topic to the 6th grade team and recommended I refer the student to the guidance counselor.

I vented about the situation to my black colleague the next day, and she expressed no surprise, but sympathy for my position (and agreed with me at the absurdity of making students request something that teachers should be asking for as a norm). I also wound up seeing the guidance counselor during fourth period (after she’d had a chance to speak with the student) & I spoke with her about the situation. She told me the student had said she would prefer if I only called her by the first name since everyone else was doing that. She said that the kid had expressed that she had wanted to try out using both names (since half her family called her both), but no longer felt comfortable doing so at school and would just keep that other name for outside school/family. The guidance counselor mentioned that she had a similar experience (she is also Latina/Hispanic). The guidance counselor was having her lunch in the staff lounge at the time of our conversation (I ran into her on my way to the bathroom, which is in the staff lounge), and she was seated with the other guidance counselor and one of the office secretaries. I mentioned how I felt angry that we hadn’t created a system to ask students about their names, and the secretary shared the story of her son’s Greek name being Americanized in school (because it is spelled differently than it is pronounced, so teachers/students made assumptions about how to pronounce his name). They all seemed relatively complacent with this situation though – it felt like they expected it and they didn’t think there was another alternative (i.e. students having their names, even “foreign-sounding” ones or double-names used and respected by people at school, people OUTSIDE of their home culture). I mentioned that I wanted to try to change the policies and how we asked students about what name to call them, and I asked if the guidance counselor could come talk to the sixth grade department about the situation. I expressed to her what my AP had said to me (that the idea might be better received, coming from an outside source like the guidance department), and she agreed, though she expressed the fact that our meetings are always during her lunch (I said she didn’t have to come for the whole meeting if she couldn’t stay). She’s (supposedly) going to come talk to us during the Wednesday meeting next week; I’ll see how that goes.

I’ve been thinking about this all weekend (my partner has heard me yell about stealing a kid’s name from her no less than three times since Friday afternoon). I think I want to propose that next year’s “summer assignment” is for each student to video themselves saying their names and their pronouns, and then the first week of school, every student’s HW is to watch the other students videos and learn the names and pronouns of the students in their classes. That’s a WAY better assignment than the “flashy” one they do now with reconstructing a puzzle cube over the summer. (I plan to propose this on Wednesday, during our team meeting).

For me, sharing this experience about what happened last week honors MLK’s work because I now understand his Letter from the Birmingham Jail SO MUCH better because of this situation (especially these specific quotes).

The first is this quote from Letter from the Birmingham Jail, “I must make two honest confessions to you, my Christian and Jewish brothers. First, I must confess that over the past few years I have been gravely disappointed with the white moderate. I have almost reached the regrettable conclusion that the Negro’s great stumbling block in his stride toward freedom is not the White Citizen’s Counciler or the Ku Klux Klanner, but the white moderate, who is more devoted to “order” than to justice; who prefers a negative peace which is the absence of tension to a positive peace which is the presence of justice; who constantly says: “I agree with you in the goal you seek, but I cannot agree with your methods of direct action”; who paternalistically believes he can set the timetable for another man’s freedom; who lives by a mythical concept of time and who constantly advises the Negro to wait for a “more convenient season.” Shallow understanding from people of good will is more frustrating than absolute misunderstanding from people of ill will. Lukewarm acceptance is much more bewildering than outright rejection.” (Emphases mine)

The second is this quote, “I had hoped that the white moderate would see this need. Perhaps I was too optimistic; perhaps I expected too much. I suppose I should have realized that few members of the oppressor race can understand the deep groans and passionate yearnings of the oppressed race, and still fewer have the vision to see that injustice must be rooted out by strong, persistent and determined action.” (Emphasis mine)

I used to be offended by his statement that the white moderate was a stumbling block for the black stride for freedom, because I saw myself as a white moderate (though now I begin to recognize I might be more of a white radical…?). I thought that surely the oppression and hate felt from active racism like the KKK was far more harmful than the passive racism from the white moderate. I didn’t get it. Until now. I see it now, in this experience with my colleague (who has been involved in courageous conversations work in the school system, so he is not unfamiliar with “the work” to be done) and being furious at him for not recognizing how expecting the students to “advocate” for themselves when he/we (the staff/faculty/teachers/admin) have the power to CHANGE the system perpetuates systemic oppression of students whose “legal” first names don’t match the names they go by (for WHATEVER reason – whether it’s due to cultural differences of having multiple first names, going by a middle name, or being transgender and using a name other than the one on the birth certificate – or even just as simple as having a nickname that feels more true to ones’ self than their legal name).

I recognized that I see the structural solution to the “issue” of mis-naming students and misusing students’ names which he was blind to. The structure that we need to put in place is to disconnect the birth certificate (and a student’s “official” record) from the name we (the teachers, the students, and the school community) know a student by, and instead, use the name that the students themselves use for themselves. In order to do this, we can restructure how we learn students names at the start of the year to ask students to tell us what names to call them (and not just SOME students whose names we read and think look “different” or “unfamiliar” but instead to ask ALL students and make NO assumptions about whose names will be familiar for US to pronounce vs. unfamiliar!). This works for students of multiple cultures as well as for transgender students. It honors students’ identities and grants them the dignity of having their names (and pronouns) respected by their peers & by the people who hold the power in their school – the teachers. We can root out the injustice of robbing students of their names not just for individual students (and thus have to keep repeating this work for each individual student), but systematically, by changing the way we interact with our students and their identities. By shifting the paradigm of student names from assumptions that the name on the register is correct or the student will advocate for themselves to asking ALL students to name themselves for us and each other, we shift the labor from a small group of students who are other-ed by the restrictive system to the entire system and to ALL students, so that ALL are on equal footing when we enter school. No assumptions made about whose names we need to repeat or practice, no assumptions about whose names will be hard for US to pronounce, but rather, an assumption that everyone has a right to hear their name pronounced correctly and be called by the pronouns & name they identify with (and that the burden should rest on the community to unpack our assumptions and biases rather than on the individuals to “advocate” for themselves in an unjust system that privileges some “familiar” names above the rest – which reminds me of this video from Key & Peele about pronouncing names according to the way a name is pronounced within a particular culture – and feels like the Ann-ah vs Ahn-na discovery from earlier this year).

My colleague, had (has?) a narrow vision of supporting our students. Instead of acknowledging that the system is BROKEN and that the SYSTEM is oppressive, he would instead teach our students to “speak up” or “advocate” for themselves – not paying attention to the weight of that (constant) emotional labor. I realized in this moment that he didn’t (as a white, cisgender, heterosexual, man) understand how heavy it is on you to continually have to advocate for your basic human dignity. I realized this is one of the ways that the “moderate white” can act as a stumbling block on the path to freedom – instead of using the power he has to change the structure of how our school learns the names to use for students, he instead has perpetuated this systemic oppression without even recognizing that there was an alternative. He told me that for 6 years this school has known that students from Hispanic backgrounds often have two names, and yet there is STILL no structure in place to ask ANY students what name we should call them.

I am beginning to learn the hard truth behind Dr. Martin Luther King Jr’s quote, “We know through painful experience that freedom is never voluntarily given by the oppressor; it must be demanded by the oppressed.” I hoped that the people at the school I currently work with (who SEEM to be open to conversations about race & inequity) would better see how to support our students, how to free our students, but instead, their vision of freedom is only within the current oppressive system, rather than re-envisioning an entirely new system/replacing the parts of the system that are broken. It seems like their vision is still limited; we’ve got more work to do. I get the sense that they’re open to doing this work (some of them, at least), even if they don’t know how. As I was bringing up the issues of trans students to this AP, during this conversation about names (and making the connections to my own experiences with names and pronouns in college and our students with multiple names), he mentioned that he had never really done any research about trans issues and wasn’t as familiar with them. I mentioned that two years ago, when I came out as trans on-stage at my school’s annual GSA assembly, my principal commented to me afterwards that she learned she was “cisgender” that day. He said I should be proud of that and making those changes, but I said that it wasn’t my job to educate her about that. She should’ve been doing that work on her own – and I recognized in this conversation what my fellow colleagues who are Educators of Color experience on a regular basis. People who are well-meaning and congratulate you for educating others, not recognizing their privilege and power in the situation means THEY should be one the ones educating themselves and advocating for people with less power than they have (both centering those people’s voices when it’s relevant, and helping to bear the emotional load of advocacy when possible). Shortly after this conversation with my AP, I saw the threads on twitter about something that seemed too similar (I can’t recall now what I posted this in response to, and it’s no longer attached to the thread it came from… Maybe it was about the incident this weekend with the Native Elder & the MAGA bigots?), but I tweeted, “It isn’t the oppressed’s responsibility to educate oppressors. It’s the responsibility of allies with privilege & power to use it to educate others who are (unknowingly) supporting oppression. Placing that responsibility on the shoulders of the oppressed perpetuates oppression.” And I recognized the analogy to what happened in my school there in tweeting that. So I’ve been considering what my role as a teacher with privilege and power is towards my students and my colleagues.

I’ve begun to realize how I’ve been complicit in white supremacy by not better educating myself about the history of racism and oppression in this country, by not having read more Dr. Martin Luther King, Jr, more James Baldwin, more Audre Lorde, more Maya Angelou, more authors of color. I’ve said before (including in a facebook post recently) that I cannot remember a SINGLE black author whose NOVEL we read IN-class (and then analyzed, etc.) from grades K – 12!! And I remember A LOT of the books we read, including the Joy Luck Club (by an Asian-American author, at least one non-white author?). I don’t even know that I ever read a book by an African until college, when I took a human resilience class (taught by my first black teacher! Senior year of college!!) and we read several memoirs by black people (including the books, Warriors Don’t Cry and A Long Way Gone). I do remember reading excerpts of books (like Other People’s Children by Lisa Delpit) in other college classes by Black authors (and other Authors of Color), but I had such a white-washed upbringing, despite growing up in Queens (one of the most diverse counties in the country!). Now, thanks to the #DisruptTexts movement, I’m way more intentional about seeking out a variety of stories in my media consumption, so I don’t fall into the trap of the “single story.”

My reflection on this experience last week and how it relates to the teachings of MLK bring me to thinking about a different quote that I first heard as an undergrad in college from the Office of Service Learning. The office was run by two people who seemed to truly understand that “community service” couldn’t begin and end with a one-time contribution, but that service to the community required understanding the community, becoming a part of the community, and figuring out what the community needed from you in order to support them. The quote was this, “If you have come here to help me, you are wasting your time. But if you have come because your liberation is bound up with mine, then let us work together,” from Aboriginal activists group, Queensland, 1970s. I see this quote as connected to a different quote from MLK’s Letter from the Birmingham Jail, “Injustice anywhere is a threat to justice everywhere. We are caught in an inescapable network of mutuality, tied in a single garment of destiny. Whatever affects one directly, affects all indirectly.” (Which, as an aside, I’ve included in my family’s Social Justice Haggadah, inspired by my first Social Justice Seder with Rabbi Mike in college).

For me, it was recognizing the oppression and injustice that I face as a transgender and queer person is tied up and connected to the oppression and injustice that people of color face (in my school’s case, the Hispanic students, in MLK’s speeches, the black people of America). While it is uncomfortable to admit, I was very much raised with the “white savior” complex (thanks to parents & ten years in Catholic school in Queens, NYC), and that influenced the ways I saw some of my students in the past. It’s unfortunate that it took me feeling the weight of oppression myself to understand others’ oppression, because if that’s what’s required to feel empathy, then we’re in trouble. I have begun to realize that it is my job as a white educator to support and push my colleagues and my students in doing this work of unpacking our biases and recognizing systems of oppression (and how we can be complicit even while not thinking of ourselves as racist). It is my job as a white educator to amplify my colleagues’ of color voices & ideas, and to decenter myself and my own experiences.

I have begun to grow through my intentional expansion of my teacher twitter network. Although I originally “insisted” it was only going to be for math educators and following math education, once I began following the José Luis Vilson & Marian Dingle, I quickly realized that there’s no way to keep social justice out of my education and still honor my students’ identities and dignity. From my conversations with them, as well as through following EDUColor on twitter, the #DisruptTexts twitter chat run by Tricia Ebarvia, Lorena German, Dr. Kim Parker, and Julia Torres, and #CleartheAir twitter chats, run by Val Brown, the resources from Tolerance.Org & voices like Shana White, Julie Jee, Absurdist Words, Ebony Elizabeth Thomas, Clint Smith III, Chris Emdin, Tsɔɔlɔ Awo, Kelly Wickham Hurst, Chanda Prescod-Weinstein, Nikole Hannah-Jones, Melinda D. Anderson, Dr. Kim Tallbear, Dr. Debbie Reese, Leslie Mac, Cornelius Minor, Sara K Ahmed, and so many more than I can name in the time I have tonight (if you’re not directly following BIPOC on your social media/news consumption, though, you need to diversify the voices you listen to and amplify), I’ve begun to recognize the work I still need to do to be anti-racist in words AND in actions. I’ve begun to distinguish between my intentions (which may be “good”) from my impact (which may not be good for ALL people), and analyze both to make sure I’m having the intended impact. I’ve watched allies like Christie Nold & Jess speak up on twitter and through their blogs (in particular, thinking about thinking about the amazing work I’ve seen Jess do with her 5th graders on her blog, Crawling out of the Classroom, and shifting the lens to inquiry about whose stories are heard and whose voices are absent). I’ve begun to be more aware of what (systemic) racism looks like, and I’ve begun to use my voice to disrupt the status quo, challenging people (students, educators, family, tweeters, etc.) who are ignorant to the impact of their actions or inaction. The more work that I do, the more I recognize how much more work there is to be done (on myself included). I’ve learned to question my own assumptions, my own biases, and my own blindspots and complicitness in racism.

I’ve read and thought about twitter threads like the following about whiteness & equity work in schools & how to stop being complicit and start being a disruptor:

https://twitter.com/Ebonyteach/status/1087048314502156290

If your equity work in schools does not involve shifting power, resources, access, or opportunities to an underserved or under supported group, you are not doing equity work in schools.

Thanks for coming to my TED Talk.

— Naysayer Please….. (@ShanaVWhite) December 8, 2018

https://twitter.com/mrsjjee/status/1087000672451657728

 

I encourage you to seek out voices like these and listen to them, think about them, and begin to do this identity work on yourself, ESPECIALLY if you’re an educator, so you can then support your colleagues and students in unpacking & examining their assumptions and biases and their impact in the classroom. Here’s a link to the next website I’m going to be reading about how to dismantle white supremacy in our schools. I’m doing some learning right now about understanding Culturally Responsive Teaching & the Brain by Zaretta Hammond (reading the book & taking an MfA course on Building & Rebuilding Authentic Relationships that references it).

I shall end this post with one of my favorite quotes from Rabbi Tarfon, also quoted in my Haggadah, that I find reassuring when I am feeling overwhelmed by oppression and how far we still have to go. This quote originally appeared in the Pirkei Avot (Chapters of Fundamental Principles) as part of the Mishnah (Jewish Oral Law), and simply states, “It is not incumbent upon you to complete the work, but neither are you at liberty to desist from it” (Avot 2:16).

Equal vs Equivalent #MTBOS #iteachmath

I’ve been a part of several different professional development sessions this year that have spurred my thinking about the distinctions between equal / equality and equivalent / equivalence with regards to math.

It started brewing in my mind because my school’s math department wanted to investigate how we develop the notions of ratios and proportions across the grades and how we develop the notions of equations and expressions across the grades – and we discovered the ideas of equivalence and equality came up in both discussions, so we expanded our view-point to see RP & EE as applications of equal vs equivalent.

I also have been thinking about the lesson from Illustrative Mathematics’ 6th grade curriculum entitled equal vs. equivalent: https://im.openupresources.org/6/teachers/6/8.html

In that lesson, they use these words to distinguish between equations which are true for ONE value (because the two expressions are EQUAL at that particular point) from equivalent expressions where they are ALWAYS true at any point. With regards to equations, it becomes clearer to see that if both sides of an equation are ALWAYS true, we would say it has infinitely many solutions. We could relate it to the graph of two equivalent lines and see that they would result in the same line.

In thinking about solving an equation algebraically, though, I can also think of creating EQUIVALENT equations (by using the properties of equality) where we simplify the equation on both sides to eventually isolate the variable, and discover the singular value that makes the equation true. For example, the equations 24 = 3(2x – 4) and 6x – 12 = 24, and 8 = 2x – 4 and x – 2 = 4 and 2x = 12 are all equivalent equations (meaning the same value of x will make them true). With some prior knowledge of algebraic manipulations, one can see how multiplying, dividing adding and subtracting can create those equivalent equations, which have an equal solution. However, one might not consider the equation 5x – 4 = 26 to be equivalent, since it’s less obvious how to transform the above equations into this one, however, if we consider “all equations with the same solution to be equivalent” then it would be, since x ALSO equals 6 when that equation is true.

However, the idea that my expressions are equivalent (instead of merely equal at one point) comes up when we apply other properties, such as the distributive property, the commutative property or the associative property, to show that various expressions are equivalent. For example, the expression 3(2x – 4) is equivalent to the expression 6x – 12 because they are the same for ALL values of x. If we “set them equal” and wrote 3(2x – 4) = 6x – 12, the equation would be true for any value of x.

From these examples and discussions, I began to see a distinction between when two expressions are EQUAL vs when two expressions are EQUIVALENT.

Then I started thinking about ratios and proportions and equivalence. We would say that the ratio 2:3 is equivalent to 4:6 or 40:60, but we might not say those ratios are equal, because they are NOT identical and they are not the exact same, though they describe an aspect of the relationship that must remain the same. Even with fractions (whether they describe a part-whole or a part-part relationship), I can think of two different fractions as being equivalent, but I’m not sure we would describe them as equal, even though we might use the equal sign (2/3 = 4/6 = 40/60, but those are equivalent fractions, not EQUAL fractions).

We also might say that there are equivalent ways to represent fractions in decimals and percents, but I’m not sure if we would describe THOSE as equal either! For example, if I have the fraction 2/5, I could also describe it as 0.4 or 40%, but are those equal or equivalent?

This made me wonder if there are ANY times when we can think about ratios and proportions from the EQUAL sense, rather than just noticing equivalence among ratios.

Kara Imm led a PD last Wednesday with “Meeps” and “Bleeps” that made me think about this distinction more deeply. On an imaginary planet, 32 meeps had the same length as 24 bleeps. We discussed that this meant that the ratio of Meeps to Bleeps is 4 : 3, and that we could even say it with fractions: 1 : 0.75 or 1 1/3:1. But when it came time to write the equations to convert from meeps to bleeps, many people fell into the “reversal error” and switched where the numbers went, saying that m = 0.75b instead of b = 0.75m, which made me recognize that there were two distinct quantities being counted/measured here: the NUMBER or AMOUNT of meeps and bleeps and the LENGTH (or size) of meeps and bleeps. In our ratio table, we had been considering the ratios of the NUMBERS of them, but when we drew a ruler to show the lengths and an equation to convert from one to the other, we needed the variable to represent the AMOUNT of them, so that the expression 0.75m would be equal to the length of a bleep or 1 1/3m would be equal to the length of a meep.

It made me have a new understanding and appreciation for why it’s so tricky for people to distinguish HOW we’re using the letters (as variables or as units), and how we’re using the equal sign – as a symbol of equality or as a symbol of equivalence!

I also made a connection between these ideas and geometry, how in geometry, the “objects” themselves (the angles, line segments, etc.) are only ever said to be either congruent or similar to another one, but the MEASURES of those objects (the measure of the angle or the lengths of the line segments, etc.) are equal. I wonder if that’s a helpful distinction here as well…

I also started thinking about the classic “coin” problems where you talk about the number of coins you have and the VALUE of those coins and try to find a solution… Writing a system of equations for that is often a challenging problem, because the coefficients of each variable in the “value” equation is implied by the type of coin used.

So now I’m wondering whether it EVER makes sense to discuss ratios as being equal, or if they’re only ever equivalent. What are other people’s thoughts?

 

A couple of the links that I read that pushed my thinking as well:

https://math.stackexchange.com/questions/1058596/in-plain-language-whats-the-difference-between-two-things-that-are-equivalent

https://english.stackexchange.com/questions/317782/equal-vs-equivalent-finer-differences-in-meaning-and-usage-in-4-distinct-scena/317792

http://mathforum.org/library/drmath/view/73189.html

Difference Between Equal and Equivalent

 

The Problem with using Acromyms & Mnemonic Devices

I saw this on Facebook today, and it really set me off: (I actually really dislike the accompanying article’s explanation, as I think it still perpetuates the problem instead of ACTUALLY developing the depth of understanding necessary):

Problems like this are why I appreciate the Boss Triangle & the NCTM’s article, “The Problem with PEMDAS.” It drives me nuts when people try to talk about math as being arbitrary based on examples like this. What I REALLY think these “viral math problems” illustrate is a lack of numeracy and a lack of understanding of the relationship between the mathematical operations AND an over reliance on mnemonic devices/acronyms to remember procedures… but, those mnemonic devices actually mask the inherent relationships necessary to figure it out (because, as Pam likes to say, math is figure-out-able).

If you understand division to be “multiplying by the reciprocal,” and you convert the divison by 2 to be multiplying by 1/2 (and thus .5), then there is literally no question that the value is 9.

You get 6 * .5 (1 + 2) as your new expression, and you now have flexibility in how you evaluate it: whether you start by taking half of 6 (which is 3) & then multiplying it by the sum in the parentheses (also 3), the product of which is 9, or you distribute the half to the two terms in the parentheses and get 6 (.5 + 1), which is 6 (1.5): still 9. There are no longer possible paths to get 0, 1, 3, or 6, which are the common “wrong answers” when trying to evaluate the original seemingly ambiguous expression. (And, if a mathematician WANTED you to divide by the PRODUCT of 2(2+1), they would have used a vinculum, often known as the “fraction bar” and put that whole expression in the denominator, with only the 6 in the numerator – grouping symbols also help mathematicians to be less ambiguous I. their intentions).

The REAL problem here is that people do not develop a deep enough understanding of the relationship between the operations to understand the ORDER of the operations. And instead of taking the time to fully develop those relationships, we fast forward students through relationships and to procedures.

The order of operations is NOT arbitrary, it is based on two key relationships:

Addition & subtraction are inverse ops & Multiplication & division are inverse operations (and radicals & exponents are inverse operations), and thus you can rewrite any radical, division, or subtraction as its inverse operation. For subtraction, use the additive inverse with addition or for division, use the multiplicative inverse (often called the reciprocal) with multiplication. You can even write radicals with fractional exponents: in this case, you indicate the inverse operation by using the multiplicative inverse of the exponent (i.e. root 2 is with an exponent of 1/2, which is the multiplicative inverse of 2, which is the power you’re trying to “undo” by taking the square root).

Thus, in considering the order of operations, you actually need only consider exponents, multiplication & addition. This is step 1 for deepening your understanding, because it explains why “PEMDAS” should actually have the MD and AS on distinct levels of the hierarchy: they are equivalent to their inverses in the order because you can eliminate division and subtraction by replacing them with M & A.

Secondly, the operations are prioritized in order of power: more powerful operations are done first (hence exponents are done before multiplication and multiplication before addition). I define powerful here to mean the operations that would change a number more if the specific numbers in question were kept constant: for example, ab will change a more than a+b, and a^b will change a even further (certainly for the integers, and even the rationals, but I think this is true for all real numbers). (I use “change” in a large part here to mean the difference between your sum or product and the original a).

I like explaining this relationship as being about power, because then it holds true even with the rationals, but students with less experience with the operations may find it helpful to also consider the fact that exponential notation (with whole numbers only) can be rewritten as repeated multiplication, and multiplication (of whole numbers) can be rewritten as repeated addition (of whole numbers). I hesitate to ONLY use that (even with kids who have less well developed relationships between the operations), because this type of understanding of the operations limits a more in-depth understanding of rational number arithmetic (i.e. addition, subtraction, multiplication, division, and exponentiation of numbers with fractional/decimal/negative parts). But that’s a whole separate issue.

Grouping symbols, like parentheses, often get thrown in to the order of operations as “coming first,” but actually, that is not at all a correct or complete understanding of the meaning or use of grouping symbols!

I also think it is confusing that we use parentheses (and brackets and braces) to group expressions together (within) and imply multiplication between quantities (one inside and one outside the parentheses), as people have to first ask themselves whether the parentheses mean multiplication or “group this expression together and treat it as a single quantity” – or worse, both meanings simultaneously!

Now, the truth is, grouping symbols are NOT required to be dealt with “first,” rather, it is that the terms/expression contained within a grouping symbol must be treated as a single quantity rather than each part of that expression treated as separate quantities that are “free” to be operated on by other parts of the overall expression.

That’s why you need to either simplify the expression inside the parentheses and then multiply OR use the distributive property to distribute the “divided by 2” (as a factor of 1/2) before you can do anything to the 1 and 2 inside the parentheses (in the original expression that inspired this post today). This could bring me to a rabbit hole about how we don’t deal with quantities that are not single numbers well, but that’s a whole different post! For now, I will simply say that experience with growing patterns and treating “chunks” of the visual as a being represented by a single can support the development of this type of understanding.

Which brings me to the last point about the order of operations: you can use the properties of numbers to make equivalent expressions: associative, commutative, distributive properties… all of which apply to MULTIPLICATION & ADDITION (but not division & subtraction), which is the other reason why if you convert the division and subtraction to multiplication and addition, the expression becomes easier to evaluate (and not as ambiguous). Both subtraction & division specify a left to right order inherent in how we record them (we do something differently to the subtrahend and the minuend or the divisor and the dividend), but because addition and multiplication are both commutative and associative, we simply call ALL of the chunks of them by the same name: factors in multiplication and addenda in addition.

These “viral math problems” are only ambiguous to evaluate if you DON’T understand the RELATIONSHIPS between operations and instead rely on acronyms and mnemonic devices to remember “what to do.”

I think if we spent MORE time on developing an understanding of these relationships between numbers and relationships between operations, we wouldn’t need to “teach” the order of operations at all: it would be a logical conclusion to these questions. It would be “figure-out-able.” In fact, if I were to sum up what I’ve learned from my work with Pam Harris, I think it directly connects:

If we develop a deep understanding of RELATIONSHIPS & QUANTITIES, then math is figure-out-able.

(And, typically, the development of that understanding comes from repetition of a relationship or a quantity & analyzing the patterns seen in the reptition OR looking for structure within quantities or relationships>> now I’ve connected the three avenues of thinking from Amy & Grace to Pam Harris’s work).

Oh, I also just felt some sparks connecting my ideas from this to the ideas that numbers represent either quantity or a relationship & the ideas of “math as a second language” & the ideas of adjective-noun that were recently shared with me on twitter… but that connection will have to wait for another post.

More Math Intervention @pwharris

So I am doing something new and unusual at my middle school this year. My school has school-wide intervention periods three times a week (we call it cerebral diversity or CD for short). CD is right after lunch, and the class is in smaller groups than a normal class for MOST of the groups (I have 12 students in mine). Students are sorted (somewhat) based on their state exam scores from the previous year – students who are at or above grade-level get to take “electives” like physics, school blog, or debate, while students who are struggling readers often are placed in intervention groups like “Just Words,” “Wilson Reading,” or “Small Group Reading Instruction.”

There are only two of us doing math intervention. The other person is trying something new this year – he’s pulling students out of other groups (primarily reading intervention) for 6-weeks at a time to use Math IXL for students to practice skills they need.

I did a completely useless intervention last year with some online program, and I don’t think any of the kids moved in their landscape of understanding or in their test scores. So I decided to try something new and different. This year, I confess, it’s a bit rocky and there’s no over-arching unit plans yet, because I’m making it up as I go along. I always take the “three-year view” with new curriculum though: the first year is a complete hit or miss mess because you don’t know what you’re doing yet, the second year is when you start getting the gist of the unit plans and order of the skills correctly, and the third year is when you really refine and hone the individual lesson plans. Even then, I think it’s really a good 5 years before you become proficient at teaching a course (this is why I think every teacher should teach the exact same course 5 years in a row, but I digress).

So I’m in my first year of this curriculum, and I’ve never had the opportunity to design a class like this before – so I’m super excited! I think it’s actually going to be profound, both for me (in the long run, having developed this class, I can then share it with other teachers in my school and/or other teachers/schools in my city or even around the country, I suppose – though it’s focused specifically at sixth graders who enter middle school without fluency and proficiency in math).

I started out with a few basic goals that I outlined in my “unit plan:”

Year-Long Essential Question

How can I set goals and grow as a mathematician?

Essential Question(s)

How can I make sense of math problems like a mathematician? How can I notice, describe and analyze patterns? How can I reason abstractly and quantitatively? How can I look for and make use of structure? How can I look for and express regularity in repeated reasoning? How can I participate in a community of mathematicians?

Unit Description

Math Cerebral Diversity is where targeted mathematics instruction lives. Each CD should aim to: Engage students as mathematicians Help students grow as mathematicians Create a mathematical community Engage students in noticing and wondering mathematically Develop students’ avenues of thinking for solving problems by providing opportunities to engage with a variety of problems Develop a bank of “ask yourself” questions and actions to take when attending to quantities and relationships, organization or behavior of number and space, and repetition in processes or calculations Expectations: Set a serious and warm tone that takes advantage of every minute this small, special group is together with you.  These groupings are time and money intensive for our school AND worth it. Match students to interesting and engaging mathematical inquiry. Confer with your students about their problem solving process and strategies. Collect and assess problems. Maintain notebooks and/or folders for student writing about their problem solving.

I had some ideas right from the start of things I wanted to include and incorporate. The first thing was that I know I want to reinforce some of the routines I use with the whole class in math instruction, where I have the students notice and wonder, or I have the students notice, describe, and generalize patterns. I knew I wanted to use games, though at the beginning, I didn’t know which math games I would use (I’ve now built up some of a list). I also knew I want to emphasize vocabulary (unit-specific and math in general), as well as support the skills/topics we’re doing in “regular” math class AND support their numeracy (my bigger focus).

Some of the routines I either plan to use (or have already begun to use) with these students: notice/wonder, three reads, problem strings, I have/you need, the routines for reasoning, rumors, and one I call “fancy date.” I also plan to use lots of math games, and I have started to grow my list: “How Close to 100?” from Jo Boaler (a dice-rolling, area game), I have/you need?, and today, KenKen. (I also plan to use something called “find the Factor” /twisted tables eventually, but I haven’t gotten there yet). I realized that Kenken’s whole advantage is that it supports students in practicing number facts (but in a puzzle/fun way!), which is BASICALLY the goal/point of this course for me. So today, I taught them how to play Kenken in the most basic of basic ones – just addition and just a 3 by 3 and a 4 by 4. Tomorrow, I’m going to give the kids MORE practice with the KenKen puzzles, and I’m going to start administering the MRI interviews tomorrow while the kids work on the new puzzles (since they can work semi-independently).

What’s the MRI, I hear you ask? I discovered (through twitter) Marilyn Burn’s Mathematical Reasoning Inventory. I’ve had students complete the written portion (I was absent for a day, and I needed sub plans!), and now I need to perform the interviews with the kids to assess their reasoning and strategies for solving the arithmetic mentally. Since there’s 12 kids, it’ll take me some time to interview them all, but I figured now that they know a puzzle/game that they can be relatively independent on, I can start conferencing with them individually/in small groups to gather the data.

Ultimately, I would love to be able to assess where the struggling students are along Cathy Fosnot’s Landscape of Learning (for addition/subtraction, multiplication/division, fractions/decimals/percents, geometry, and algebra, and statistics >> but I don’t know that those all EXIST yet!), and then track how they grow over the course of the year. I’ve accepted that this part is probably a year 2 or 3 goal; I’m not sure yet how to gather this data, and I haven’t been doing it thus far!

Now, the other component that I haven’t talked enough about is Pam Harris’ work. Maybe you’ve heard me post about her lately? I have been taking one of her online courses (this one is about developing powerful multiplication), and it’s totally influencing the way I think I’m going to design this class moving forward this year AND how I’m going to restructure it for next year.

First, I introduced the game “I have/you need” last week and did a little bit of formative assessment – one of my students even asked for it today! (we ran out of time, so we’re going to try it again). I noticed from that game that two of my students didn’t know their “pairs to ten” yet – and many of them struggled with the pairs to 100 that weren’t “easy” (heck, I even struggle with that – that’s why I’m so much slower at mental math than my partner – she knows all of those pairs to 1000!). I had heard about this game before, but Pam’s website nicely laid out exactly how to begin and how to structure this game so it gets progressively harder and so that the kids start to build fluency with some of the facts.

A second thing I’ve been learning about (from her multiplication online course) is the different strategies for multiplication. She has 5/6 strategies that she says are VITAL for kids to know to be able to efficiently solve any problem that’s reasonable to solve without a calculator. The strategies (as I’ve understood them so far from her) are basically broken into two types: the ones that use the associative property (and maybe also the commutative property) and the ones that use the distributive property. She has named them doubling and halving (which can be extended to tripling/thirding, etc), and then flexible factors (where you can actually change the numbers you’re multiplying by rearranging the factors – for example, 6 x 35 can become 21 x 10 because 6 = 3 x 2 and 35 = 5 x 7, so the 5 and 2 can be regrouped and the 3 and 7 can be regrouped, and the 21 x 10 is MUCH easier to do mentally!) and then there are three types of chunking: “smart” partial products (to be distinguished from the four-part “place value” chunking prioritized by the algorithm), 5 is half of ten, and over/under (where you go to a friendly number that’s a little above or below your target and then adjust with addition or subtraction). Once students have the idea of a fraction as an operator, you can also use “quarters” as a strategy (this would mostly be an associative property one), where to multiply by 25, you could divide by 4 (or halve and halve again) and multiply by 100. She mentioned that some of the strategies come sooner on the Landscape for learning, and that would also support kids in mastering them first (it gives us, as teachers, an idea of the “usual progression” through the ideas, so we can support students in moving forward into more efficient/sophisticated strategies as they get stronger with the concepts and skills).

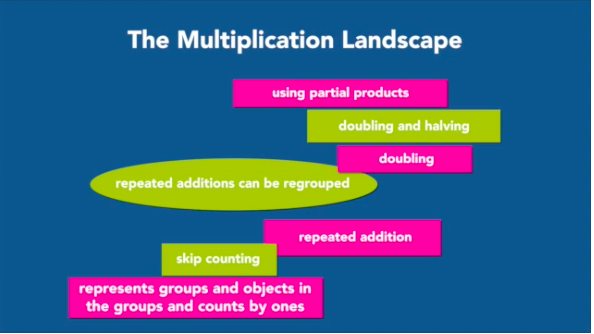
So then tonight, Pam also mentioned two big ideas (plus a bunch of littler, supporting ideas) in the class that I want to incorporate into my planning for CD:

First, the associative property-based strategies are easier for the kids to own because it “stays” in the multiplication whereas the chunking requires the students to know WHAT they’re adding or subtracting (which, when we keep it in a context like packets of gum, they can make sense of), but doubling is lower on the landscape of learning, a chunk of which is shown above, so they’re more likely to master that first. So this made me start thinking about the best order to introduce the strategies (via the various strings). I tried to do a x9 strategy with my kids the other day, and they seemed like they were starting to get it in the moment, but when I tried to revisit it the next day, they hadn’t retained it. And when I shared that with Pam (and Kim and Sue, and a few others at the end of tonight’s course), they reminded me that of course students hadn’t integrated it yet! It was brand new to them, and in the same way that I wouldn’t expect students to have mastered anything else after only doing it once, I need to do problem strings to develop a particular strategy more than once with my kids as well! Which brings me to a related idea, which is that we want to order the strings so that they’re developing the strategies in a manner that the kids can master them – but also so that the kids get enough experience with the “type of strategy” (and both the ratio table and array models) to be able to “own” the strategy and the ideas behind it. All of this reassured me that they will eventually master the x9, as long as I keep revisiting it. But it also made me realize I should use the landscape of learning to my advantage & start with an easier strategy to master, like double, double, double.

The other thing we discussed tonight were the “basic facts” and how to have strategies for each of them. She even sort of went in an order that seemed like it could be the order that I introduce it to the kids. Here’s what I heard. 

To support our students learning their multiplication facts, we need to focus in on one type of fact at a time, developing strategies for that number. She highlighted in color as she went through. My understanding of the order (for the 1 – 10 facts FIRST) is that kids should understand what it means to have “zero groups” of something >> and then what the zero facts are. They should next understand what it means to have “one group” of something >> and then they need to own the one facts. (I think that might be part of my conversation with the kids tomorrow, before we start playing Kenken, after we’ve played “I have, you need”). Then, they can move into doubling (x2), doubling and one more group (x3), and double-double (x4). From there, she suggested skipping to double-double-double for (x8). Then we went up to the x10, which is a place value shift. I was actually surprised in some ways that we had waited so long to get there, but I realized that noticing the place value shift is harder than just skip counting by tens or “adding a zero,” so I actually think it makes sense to develop some multiplication understanding before going to the times ten – because now, I could see an array that was n by 1 being repeated ten times to show the 10n. From there, she moved into the idea that 9 is 10 groups minus one group and then that x5 is half of times ten.

These strategies (combined with recognizing the symmetry in the table and that ultimately, you can “reverse the order of the factors” without impacting the product – the commutative property) reduce the number of facts you might need to “memorize” down to three facts: 6×7, 6×6, and 7×7. For some reason, she said 7 x 7, the kids often seem to know, but then we could think about how else to support kids in learning these facts. And I discovered my new favorite for 6 x7. If you know 3×7 = 21, then doubling the 3 to get 6 means we can double the 21 to get 42 (and 21 is pretty easy to double!). We can actually continue that pattern to do 12 x 7, where we can see that we’re doubling the 6 to get 12, so we can again double the product, which again is pretty easy – 42 doubled is 84. So now we’ve not only gotten the ten-times table, we’ve already started thinking about the 12 times table.

I’m guessing that the “elevens” are going to be using chunking of 10 groups plus one group (sort of like the “opposite” of the nines).

The 12s, I can see in a few ways:

1. Reverse the facts >> instead of trying to remember 12 x 2, remember 2 x 12. This works for the easier ones on our list like 1, 2, 10, 5, and maybe 3, 4, 6, 8.
2. Combine a few of the strategies: double to find x2, add one group to find x3, and then double (to find x6) and double again (to find x12). OR, if you already “know” some of those facts, then to go back to them and work on those individually.
3. Chunk it into friendly numbers (like x10 + x2)

I actually just thought of another “game”/routine we need to do in my CD. We should do the choral count-arounds (or other ideas) or whatever they’re called. I just thought about how powerful it would be to get kids practice “doubling.” What if we started with a number, and I said “15. Now double it.” and then pointed to kids in our small circle, one after the other, and they had to double the previous number (in this case, 15, 30, 60, 120, 240, 480, 960, 1920, ahh!) instead of just doubling for powers of 2!

This is basically my attempts at consolidating some of my learning from tonight’s multiplication session, and to connect it with the work I’m trying to do in my CD. I’m also simultaneously “planning” for tomorrow and this year!

Oh, I just remembered another thing Pam mentioned – she talked about how to use flash cards (and now I’ve gotta check and see if I can find my deck – I hope I didn’t get rid of them!). Use them to categorize whether a student “just knows” a fact or if they don’t have it mastered yet (split the deck into “mastered” and “not mastered” in an interview style). They’re not racing, but any that they don’t know in about 3 seconds, put in the “not yet” pile. Then go back through and make a “clue card” based on strategies they know. For example, if they struggled with 8 x 7, maybe they want the reminder “7 = 5 + 2” or maybe they want the strategy “double-double-double” or maybe they want to try “double 7 x 4” because they know that. They’re building on relationships they know.

There was also the practice with connecting the multiplication problems on the paper (instead of using a “mad minute” with timer and doing as many as you can!), and I really liked that idea too!

I think my goal for my students is to start by simultaneously developing their pairs to ten and pairs to 100 (to support their additive reasoning and move them from counting), as well as to develop their multiplicative thinking, by mastering these strategies AND by mastering their facts. Because the COOLEST part (imo) is that a kid who has a strategy like “5 is half of ten” now owns not JUST the first 12 multiples of 5, but ANY multiple, because they have a generalizable strategy that ALWAYS works. So if I say “13 x 5” they can do 130 / 2 = 65. If I say, “24 x 5” they can say “240/2 = 120.” Now yes, this requires them to have mastered doubling and halving – which is why I think this brings me back to where I’m going to go next.

Tomorrow, we’re going to do more KenKen puzzles & I’m going to start doing assessments of the students. I’m going to do as many interviews as I possibly can & I’m going to try to record the ones that students know/don’t know and/or their strategies (I haven’t decided whether I’m going to start with the MRI from Marilyn or just the multiplication facts like Pam suggested. I’m going to try to record where kids are for the addition pairs while we play a game of “I have, you need” to warm-up immediately after lunch). On Thursday, I’ll probably do the same exact thing so we continue until we finish the MRI/interviewing of the kids.

Once I have that mastered (probably by next Tuesday), I’m going to continue developing their pairs to 100, but also shift to focusing on the multiplication facts. I’m going to start with ensuring that we’re solid with a rule for x1 and x0 (I THINK we are, but I am making NO assumptions anymore!). Then, we’re going to work on doubling until we have it mastered. We’re going to work on doubling both with strings that will show us double, double = x4 and double double double = x8, and also doubling to build on x3. I’m wondering how to support kids in “mastering doubling” though for kids who don’t have that skill yet (Pam? Any thoughts?). That may be more of an “elementary” skill, and maybe some of them have it more than I think, but I also know the “pairs to 10, 20, 100, 50, etc.” will make the doubling easier. I also wonder if I might need to go into compensation for addition strategies, or if I should just leave that be for now…

Once we’ve mastered doubling, we’ll work on the chunking for times three – double and add one group, double and add one group, etc. I also think at this point, it’ll be important to practice halving – though I’m not sure exactly what to do yet here (especially, since I had a few students who struggled to recognize even numbers that were three digits or four digits!). I also want to show some of the strings of doubling and halving here, so the kids recognize that sometimes, it might be easier to make a problem into a related but easier problem (i.e. 18 x 5 is kinda yucky, but 9 x 10 is easy – and you’ve essentially taken a factor of 2 from the 18 and given it to the 5 >> which KINDA reminds me of the compensation strategy from addition, where if you were adding 18 + 5, which is kinda yucky, you might take 2 from the 5 to make the 18 into 20, and then do 20 + 3 instead).

I think once they know how to double and halve, we’ll move into 5 is half of ten (because they already have some fluency with the times ten and we discussed it in terms of dollar bills the other day), and then ultimately, we’ll revisit the 9s and 11s, thinking about the chunking strategies at that stage.

I want to shift the kids away from skip counting, and I want them to start thinking multiplicatively. I think this order might get us a pretty good start. Let’s see how we go.

Finally, the last thing I was thinking about was something that came up after the main session, in my conversation with the smaller group of folks who stuck around (yes, I’m THAT kid! No, you’re not surprised!). I mentioned how we had done a string for the 9s strategy on Wednesday last week, and when we came back on Thursday, they didn’t remember the strategy at all. And one of the teachers reminded me that it takes repeated exposure to the strategies before the kids own them, and I was like “Oh, duh! I know that.” But it helped to remind me that the kids need more experience with thinking about the relationships and making sense of the math, and not just being expected to catch up “all at once.”

One last thing (and this was influenced by Grace & Amy, so let me give credit, where credit is due). Their routines (because of the annotation on the posters) wind up leaving a tangible “remnant” that can be used as an anchor chart. They also have the routines end with a meta-reflection, so the kids think about what they saw today as being connected to a future problem. The prompts often say things like,

“When doing <a>, I learned to pay attention to…”

“When doing <a>, I learned to ask myself…”

“The next time I do <a>, I will…”

That might also help them retain more, because it tunes them in and helps them think about the critical parts that relate to future problems.

Alright, that’s it for real now.

Middle School Intervention that Works

I was rambling about my small group intervention to my partner, Charlie, tonight, and it was suggested that I should blog about this because it’s important to capture these ideas in writing. So here goes.

I’ve been thinking A LOT about designing a small group intervention in math that really support kids in the transition from elementary school to middle school. In particular, I’m focused on my “cerebral diversity” group – essentially, a group of 12 students who I meet with three times a week for about 35 – 40 minutes for additional math support. I’ve been trying to think about the best ways to support them in developing their mathematical reasoning.

So that brings me back to Pam’s diagram from my last post (this is clearly stuck in my mind!):

In middle school, I want students to develop their proportional reasoning (particularly in 6th grade), so that means they need a solid foundation of additive and multiplicative thinking strategies. I’ve already started to make connections to this diagram in my observations of my students’ struggles. Yesterday, I had a student do division by drawing circles and counting (one by one!) 64 tick marks into the 8 circles (and he only knew to draw 8 circles because he saw that number on his multiplication facts handout because he doesn’t have fluency with his multiplication facts). I realized he was stuck in a counting strategy for a multiplication problem – he didn’t even have additive strategies in that moment!

So this brings me to what I did with my small group intervention this week:

On Tuesday, we previewed the idea of common multiples by looking at the 2, 3, and 5 times tables. We talked about the numbers that appeared in MORE THAN ONE table and named them common multiples.

On Wednesday, we worked on a problem string to develop a strategy for doing “9 times anything.” We started by using money to talk about place value and multiplying by 10 and 100. I asked students to consider how much money I had if I had 14 $10 bills. And then I asked them how I could trade that in so that I had fewer bills. After a few people said “and two twenties” I clarified that the bank I went to ONLY had 1s, 10s, and 100s. We then filled in our place value with 1 hundred, 4 tens, and 0 ones. We did the same thing for 27 tens and then for 27 hundreds. Some of the kids had never heard the phrase “twenty-seven hundred” to describe “two thousand, seven hundred” so we discussed that language.

Once it seemed clear they understood how to multiply by ten (and had a better sense of WHY we shift the place value than the often heard “add a zero” explanation), I decided to move into this string. We started with 6 x 10, 6 x 9, and connected the two. Then we did 8 x 10 and 8 x 9. We did 7 x 10, then 7 x 9, and then made a connection between the two. I recognize now that I wasn’t using a good model to help the students think because I was just writing multiplication sentences up there. I also wasn’t grounding us in a context, so when I jumped to 14 x 10 and 14 x 9, they got a bit stuck. There were two answers in the room for 14 x 9: 131 and 126. We used the context of gum packets and sticks of gum (which they were all familiar with from class number strings I’d done with them) to reason that it must be 126. We continued to 13 x 10 and 13 x 9 and then 17 x 10 and 17 x 9. When this problem came up, one student shared how he did the subtraction as 170 – 10 – 7, and I asked if I could represent his thinking on a number line. He agreed, and my other students saw how his strategy was helpful.

I tried to scale up this strategy to anything times 99. I had the kids multiply by 100 and then one of them even predicted we would do x 99! Only one kid was actually able to use the strategy of x 10 – x1 successfully, and got 1683.

I also noticed that some of the kids were easily doing the x10 but getting stuck on the subtraction – and I realized they might not have subtraction strategies that were helpful. So I decided to focus on supporting that with the “I have, You need” game that Pam introduced me to.

On Thursday, I tried to revisit the strategy from the previous day for multiplying by 9, and most of the students had forgotten it! I asked them how to do 19 x 9 using the strategy from yesterday and only after much prompting a few kids were able to remember we did 19 x 10 and 190 – 19. I then asked them if they could write the “helper problems” for 62 x 9 (getting 62 from one of the students) and some of them could – but not all. I decided to try to have the kids generalize, but they struggled to say the two steps were “multiply the number by 10, then subtract that number.” At one point, I said “let’s say we have ANY number, let’s call it N” and I totally lost a few of them. I realized I was trying to shove something on them they weren’t ready for, so I pivoted. Instead of doing my original plan (which was going to be to build on the x9 strategy and try out x19), I decided to play the game with them instead.

We got in a circle, and I told them I was going to start small so we could learn the rules of how this game was played. I wrote “Target = 10” and I drew the following on the board: _____ + _____ = 10. I then told them I was going to give them a number (and pointed at the first blank) and they were going to give me the pair that we could add to it to make 10. I said the numbers in a somewhat random order, 9, 8, 6, 7, 5, 3, 1, 2, and I pointed at each of the different kids. I noticed two kids were struggling with this. One of them even said he wasn’t quite sure how to play, so I filled in the first blank with the number I gave him (7), and asked him for the second number and pointed at the blank. He had to count it on his fingers.

He shook his hand “so-so” when I asked if everyone understood how to play. I said ok, let’s try it with 100, and I gave the kids ONLY multiples of ten. Most of them were pretty good, but it became clear two of the kids were counting (I hope by tens, but it was silent, so I wasn’t sure). I moved into the multiples of 5 (so giving a kid 85 and expecting 15 back), and when I tried to give one student 25, she couldn’t get 75. I tried to relate it to money for her, but while she knew there were 4 quarters in a dollar, and if I had one quarter, she would have 3, she didn’t know how much money that was worth. She could say one quarter was 25, and two quarters was 50, but froze up when asked for three quarters.

This gave me great formative assessment about where the kids were. Since we were out of time, I told the kids that they should play this game with the types of facts they didn’t know yet (I mentioned to my two counters that they needed to work with the pairs to 10 first).

As an aside: in talking with my principal & AP, they’ve talked about how the kids don’t “move” in math – in other words, their test scores are stagnant. And I felt like this experience really showed me why. In 6th grade, the students are being assessed on their multiplicative reasoning and their proportional reasoning – but if they don’t even have additive strategies yet, they’re going to struggle with that level of reasoning! So I need to support my students in getting OUT of counting and getting to higher levels of thinking.

This leads me to my ideas about designing this support curriculum. I am thinking through the three days a week I have with these 12 kids, and I’m thinking about how to arrange it so that we have one day that’s supporting their work in class (either previewing vocabulary or a skill or reinforcing something, etc.), one day that’s a problem string with multiplication strategies, and one day that’s supporting their additive reasoning and moving them out of counting. I think we can play this game with target to 100 and once I get to know the students, I can differentiate the level of complexity I can give them based on which skills I see they need to work on.

As an aside: tonight, in the conversation with my partner, it became apparent why she’s so much faster with mental math than I am: she “owns” all of the addition pairs from 1 – 100 and 1 – 1000! Whereas I own 1 – 10, and 1 – 20, I’m shaky on my 1 – 100 pairs. I own the multiples of ten (i.e. 10 + 90 or 40 + 60), but when it comes to my multiples of 5, I don’t “own” the facts close to the middle. For example, I know the 95 + 5, 85 + 15, and 75 + 25 forwards and backwards without thinking. But 65 + 35 and 55 + 45 trip me up every time. I want to say 65 + 45 and 55 + 55, and I don’t want to use 35 at all there! When I get into the “ones,” it’s even worse! I don’t know them with fluency at all!

So I started practicing them tonight! And I’m going to keep practicing them, building the level of complexity until I have all of the numbers to 100 mastered! I’m wondering whether I should share with my kids that I’m working on these too. I think there’s something powerful for them to recognize that even adults might have gaps in their fluency, but that once you recognize a gap, you can practice that skill and improve.

Additionally, I now know that next year, I want to use this “game” earlier in the year to assess who’s still counting and who’s got some of these facts mastered.

Incorporating Routines into your Classroom Culture: The Importance of Naming @RhondaBondie1 @Melvinperalta #TMCNYC18

At TMC NYC last week, Melvin asked me how I started with routines and which routines I would recommend doing first. It got me thinking about the evolution of using routines in my own instruction and so here is my long awaited reflection on his questions.

The first thing I will say is that even now, I’m still not perfect. I definitely still struggle to be consistent in my implementation and to reinforce these routines regularly. I find myself continually having to remind the students (and myself) of some of these norms and expectations. I hope eventually this year, as the kids learn these routines, it will become more clear and automatic – but with 6th graders, I’m not holding my breath!

It was when I started taking courses with Rhonda Bondie that I started considering the power of NAMING the moves of a routine so that we could be consistent, and “refer back to our play book.” If I say “that team just did a hail mary!” you probably have SOME vision of what that means, even if you don’t know much about football. In the same way, we can name OUR in-class routines with names so that if we tell students “do a Share-Check-Discuss,” they know what that means – in terms of their roles and responsibilities, in terms of the action pattern, etc.

And so I think it’s very appropriate that my routines list starts with incorporating simple ideas from Rhonda:

Confirm & Contribute – when students are sharing (either with partners or groups or even as a whole class), and we’re writing (a list, a table, etc.), I ask students who are “audience members” to listen to the idea and compare it with their own list in their NB. If they’ve got something similar, they should check it off (confirming it) and if it’s a new idea, they should write + before recording the new ideas in their notebook (contributing it to their list). This accomplishes two things: 1. it gets students listening and comparing their ideas with what’s floating around the room and 2. it gets students who didn’t come up with as many ideas on their own a list to refer back to because they’ve now copied some classmates’ ideas into their NB.

Listen for Patterns and Surprises – I pulled this out of the “talk-think-open exchange” which Rhonda does (and I never have), where I tell students what to listen for as they’re sharing something, and then I give them time to discuss with their groups a pattern or surprise they noticed. This helps them know what to listen for (and to try to make connections between the ideas they hear) and it always gives us something to share out.

While I like Rumors (in theory and with adults), I’ve rarely actually used it with students because I never seem to know HOW to deploy it. It’s a place where we should be able to share ideas around the class, and kids get to get up and talk to lots of different people, but I’m not sure that I always find a tremendous amount of value from it, as sometimes the kids just swap cards (without reading or talking) or they just try to go to as many people as possible without listening to the new ideas. So I’m not 100% I would include Rumors in my “regulars” list, but it’s in my “favorites with adults” to use.

I also like Rhonda’s Idea Carousel, but I haven’t actually used it in my classroom as a teacher yet, though I’ve experienced it as a learner and loved it! I also used it as a facilitator of PD, and I found it extremely helpful and useful as well.

I also created a routine similar to hers that I call “Share, Check, Discuss.” It’s purpose is to check work the students have already completed independently or at home and to save only the questions with major confusion for the whole class discussion. The way it works is this: in groups of 4, students choose one person to go first and a direction to go around. They each have the paper they’re checking and their pencil. The first person reads aloud their answer to number 1; the listeners either check it off that they agree OR they circle it that they disagree. They rotate, going through the whole page, just reading answers (no comments or questions at this stage). After they get to the last question, the next person should ask “What questions did people circle?” This will direct their conversation back to the problems people disagreed on. I will give each group a post-it note to record ALL of the numbers of the problems ANYONE disagreed about and then to STAR the problems they still want to go over. I use that data to choose to either go over the problems that the most groups requested OR to know if we can skip going over the handout’s answers.

So of those five routines, I’ve already taught my students the first two, and I haven’t used the last three with my students at all.

Then, I find there are some more math-specific routines that I’ve started to incorporate, like Notice/Wonder and Which One Doesn’t Belong? In my actual enactment of these routines, I utilize routines and moves from Rhonda – for example, in sharing out from a notice/wonder, I cold call students and I offer them the opportunity to confirm or contribute ideas to our list to hear more voices. For Which One Doesn’t Belong, I’ve had students move to different corners of the room and share in groups based on which section they first thought might not belong, and then I’ve had them prepare a reporter to share out the most common reasons or to share out any surprises. Alternatively, I’ve done domino discovers to ask students to share out their ideas about the WODB or even to share out the most important noticing or the wondering they’re most curious about as a group. Domino Discover is another routine from Rhonda.

I’ve done all three of those in my class this year already (WODB, N/T, and DD).

I’ve been moving from minor routines (some of which I would almost name “moves” over “full blown routines”) to more structured, whole-class routines that follow a bunch of stages, flowing from a launch into repeated patterns of individual think time – partner shares – and whole class discussions into a final reflection. I learned about this general structure from David Wees, based on the icon he has shared from the New Visions website.

For me, my first experience with these kinds of routines came from Kara Imm’s number/problem strings during the developing mathematics year long course at MfA. I explored Pamela Weber Harris’s books as well, and eventually enacted these routines, but I had trouble at first, because I didn’t have this framework in mind. Once I incorporated more partner talk, I found my flow in enacting these number talks/strings. Additionally, when I incorporated the meta reflection at the end, I found students actually took something away from those number strings that was concrete, so I found that amplified the power of it. The other support that’s not highlighted here, in this sequence, but I first really thought about from looking at David’s PPT slides was about the role of sentence starters in supporting student conversations about the math AND consistent use of iconography to indicate the roles, routines, or other constraints of a situation (such as pencils or no pencils, alone or in partners or in whole groups, looking or talking, etc.). He claims it’s out of laziness, but I actually think the consistency of that is helpful for students – now they know, if they see this symbol, this is what I should do in class!

The first two routines I learned that were this degree of structured were Contemplate then Calculate and Connecting Representations from Amy Lucenta and Grace Kelemanik. I’ve also learned the 3 Reads Strategy and I’m teaching myself the Capturing Quantities routine (because I think it builds nicely off 3 Reads, especially for 6th grade math). I learned CthenC first, but I actually like Connecting Reps MORE. In part, this is because I want to use CthenC to highlight interesting/specifically helpful strategies, but to select which students I will call on, I need to really hear their strategies – and that doesn’t always happen succinctly. That can mean that it takes me too long to select students. Whereas in Connecting Reps, I can ask them which one they connected, and know that I can ask them clarifying/probing questions while they’re presenting to highlight features of the connection they might not initially mention.

So far this year, I’ve done problem strings with my students to develop their multiplicative thinking. I haven’t yet done CR or CthenC this year, though I used both of them last year. I just launched 3 Reads yesterday with my kids for the first time, because it was the first time we really had a word problem to read through and make sense of. I hope as it becomes more routine, the students will get better at it. I had to pause with Capturing Quantities (and I’m not 100% sure I feel confident actually deploying it yet), but hopefully, I’ll try it out during my ratios and proportions unit.

I try to let my math goal determine which routine I choose, but I also know that sometimes, I’m thinking about my student “study skills” and “active participating” routines (like notice/wonder or confirm and contribute). I hope this list is helpful.

Thinking through LCM & GCF (Inspired by @pwharris visit)

Let me first make a connection to Sara Van Der Werf’s post about being an evangelist: I have come to realize that I am a problem strings evangelist (and thus to some extent a Kara Imm & Pam Harris evangelist, as I learned basically everything I know about problem strings from the two of them).

On Wednesday last week, I had the amazing opportunity to finally meet Pam Harris in person! She came to my classroom and led a problem string with my class! (can you tell I’m EXCITED?!) Then we (and my co-teacher) debriefed the lesson, and talked math, math teaching, and so much more for the next few hours! I designed a string with her then, and I implemented (most of it) on Thursday in my classes. That’s a different blog post that I haven’t written yet; the focus of this post is about this image that she shared: both on twitter and in our conversation.

Essentially, this image represents the types of strategies we have for various problems. It does impose a sort of hierarchy to the thinking, recognizing that proportional reasoning, for example, is more sophisticated than counting strategies. I then watched this video where she explains it in even more detail.

(As an aside, as I watched her video, I thought about my own strengths and weaknesses as a mathematician and my own strategies. I realized that I have pretty decent proportional reasoning because my multiplicative reasoning is good. But my additive reasoning sucks. If you ask me to add a few numbers, I don’t have as much fluency as I should. And subtraction? Oh that can be a nightmare too! But then, I heard in that video I shared above that Pam mentioned the game “I have, who has?” and knowing the additive partners to 100… and I was like, “OH SHIT. I need to do that game!” Because recognizing the other piece out of 10, then out of 20, then out of 100 – that’s how you start building your additive reasoning strategies! But again, that’s another post for another time!)

This got me thinking about how to teach my 6th graders to find the LCM & the GCF. My school uses CMP3, a problem-based math curriculum. [Aside: I do think it is very strong in many ways, though I also think it has some gaps and weaknesses. My goal this year is to think through some of the problem strings that would support my students in developing the reasoning they need to engage in these problems. I can’t even tell you how excited I am that Pam’s going to support me in making those strings and the connections/integrations within the problems/investigations! Again, that’ll probably be a future post!.]

CMP3 uses three problems to introduce students to the LCM & GCF: the ferris wheel problem, the cicadas problem, and the snack packs problem. For those of you not familiar with the curriculum, let me summarize these three problems:

In the Ferris Wheel problem, they talk about different sized Ferris wheels that complete their revolutions at different times, and therefore, the two people who get in at the same time, go past the bottom at different times… So the students are asked to calculate when the people would next both be at the bottom at the same time: this turns into a common multiples problems. They’ve selected the numbers in the problem strategically, so that you’re finding the least common multiple of 20 and 60 (which is one of the numbers because 60 is a multiple of 20), the least common multiple of 30 and 50 (which share the factor of 10, so it is 3 x 5 x 10 = 150), and the least common multiple of 11 and 20, two relatively prime numbers (so the LCM is their product).

In the next problem, the students are taught about cicadas which have prime number life cycles, in that there’s a brood of these insects that emerge every 13 years and another one that emerges every 17 years. The students are then asked to find the next time both will emerge in the same year. Because the two numbers are relatively prime (and happen to be prime!), the students can just multiply 13 x 17 to find the answer. There’s an extended problem where they have to find the next time a 12, 14 and 16 year cycle would overlap as well, which is definitely a bit of an extension at this point, as it requires noticing that while 12 and 16 share a common factor of 4, the 14 only shares a common factor of 2. This problem also pushes students to try to generalize a method for finding the LCM for any pair of numbers and predict when the LCM will be equal to the product or less than the product of the two numbers.

The third problem shifts gears and asks the students to break up food into snack packs with the same number of each types of snack (apples and trail mix bags). The numbers involved are 24 and 36, which share a common factor of 1, 2, 3, 4, 6, and 12, so students are both recognizing common factors AND directed towards the greatest common factor. After this problem, students are asked to consider when real world problems ask them to use multiples and when real world problems as them to use factors. The hope is that students see that breaking two things into equal groups will require factors, whereas two things that happen repeatedly in cycles will involve multiples.

The third investigation in the book goes into “number (factor) strings” where they push kids to move from the product of two factors equaling a number to three factors, four factors, and so on, breaking the factors down through a puzzle to eventually find the prime factorization of a number. My new school’s unit plan basically skips over the prime factorization investigation because of the combination of time and the fact that it’s not “directly” related to the standard being assessed (i.e. students aren’t asked for the prime factorization of a number in 6th grade in NYC; they’re asked for the LCM or GCF of two numbers, either in context or not, and Prime Factorization is just one strategy they can use to find those values).

However, I’m now even more worried about how to run these three problems so that my students leave with (a) having made sense of when to find factors vs. multiples, but even more importantly (b) having made sense of HOW to find common multiples & factors with strategies BEYOND JUST listing multiples and looking for common ones. Now that I have Pam’s graphic in my mind, I recognize that skip-counting is a form of additive thinking (as they are technically repeatedly adding the number to itself as they produce each multiple), and my students need to move into proportional reasoning this year – so I can’t leave them in additive strategies.  So I began brainstorming the multiplicative strategies for finding the GCF & LCM of two (or more) numbers.

I started by analyzing my own strategies for finding the LCM & GCF, and everything I could think of EITHER required knowing the prime factors of a number, involved skip counting, or (in one case) involved the Euclidean Algorithm to find the GCF and then the “LCM algorithm” (I don’t know if it has a more official name), which says for to find LCM (m, n), do mn/gcf(mn) (which is why relatively prime numbers have an LCM equal to their product – when you divide by their GCF, you divide by 1, and it doesn’t change the quantity). I wasn’t sure which (if any) of these strategies would be most accessible to my students and yet simultaneously enhance their thinking beyond just counting strategies.

So that led me to my twitter network to ask people how THEY think/teach about the GCF/LCM.

#MTBOS #msmathchat what strategies do you have for finding the GCF or LCM of two numbers? I am trying to anticipate what my 6th graders might try… and what I can do to support them in moving beyond listing multiples (my anticipation of the “main” strategy).

— Kit (@MrKitMath) October 4, 2018

And I got only a few different types of responses. I noticed there were certain trends: people used primes (either with factor trees or Venn Diagrams) or people used an “organization technique” like the ladder method/grid method/cake method. The only other thing that came up was Howie’s video.

First, I think I will try to find a way to incorporate Howie Hua’s video with my students, because I think this is a method for finding the GCF that involves subtraction and to some extent, repeated division (and actually builds towards the Euclidean Algorithm). But I do worry that it might leave students stuck in a lower level of thinking.

The tactile version of the Euclidean Algorithm:
Finding the GCF of two numbers by comparing differences until we have equal stacks.#MTBoS #iteachmath pic.twitter.com/LSsKqekFTC

— Howie Hua (@howie_hua) September 16, 2018

One method people shared for getting the LCM & GCF of two numbers was using prime factorization and then organizing the prime factors somehow (often using Venn Diagrams) to find the GCF & LCM. People had different ways of organizing their prime factorization (often the “factor trees” method), but ultimately this method was as follows:

•  Find the prime factors of each number by “splitting” it into two numbers you KNOW are factors. Repeat this until all factors at the end of the branches are prime numbers.
• Once you have the prime numbers for BOTH original numbers, circle the ones they both have (or arrange them in a Venn Diagram) – the product of all of these is the greatest common factor.
• Take the GCF and any “extra” prime factors that were unused. The product of ALL of these numbers is the LCM.

This is definitely one way to find the GCF/LCM efficiently – but considering that my school is skipping the Prime Factorization unit of Prime Time, I’m not sure whether or not my students will have the ability to use this reasoning/strategy – plus, many of my students don’t have mastery of any divisibility rules (for some of them, I even mean recognizing even numbers as divisible by 2!), so finding prime factors may not be the best method to start with. (Plus, if we were to follow CMP3, Prime Factorization comes AFTER common multiples/common factors, so theoretically, there should be OTHER methods).

The other main method that came up is called the grid method, the ladder method, or the cake method, based on the model that we use to organize the thinking involved. It all seems to be identical MATH, but different names for an almost identical “organizing structure.” Matt Coaty shared this video to explain this method.  Essentially, you look at your two numbers for common factors, and you keep dividing your quotients over and over again until the two quotients from your two numbers are relatively prime – they you know you’ve got no more common factors to “pull out” and thus, you’ve found the GCF. From the GCF, you can multiply the GCF by the two “left over” factors to get the LCM.

Watching this video was a big painful, though. The narrator/teacher  mentions how to multiply for the LCM, and it made me cringe so hard. She first doubles, doubles, doubles and doubles to get 16. Then says “you might not know how to do 16 x 7 in your head, so you can come over here and do work on the side. She then demonstrates doing 16 x 7… without actually showing any of the steps that she took to get 112! So I couldn’t help but wonder why she bothered to write anything down on the side at all! Then she does another thing I hate which is “string multiply” where she begins the next problem attached to the first problem (this teaches such horrible things about the equal sign and interferes with kids’ ability to understand it as a symbol meaning “equivalence” rather than a symbol meaning “find the answer” which is what most kids think when they first come to me in 6th grade. And finally, she gets the 560 without showing any steps again! Whereas (because I’ve worked with Pam), I started with 5 x 2 = 10, 7 x 10 = 70, and then I doubled, doubled, doubled to get 70, 140, 280, 560!

I realized that from watching this video, when they showed the L-shape, and she started multiplying from left to right, 2 x 2 x 2 x 2 x 7 which got her 112 (the original number on the left) and then x 5, and I realized she got the original number on the left from the first factors, and the only thing that was new was the 5. Instead of RE-doing the multiplication, she should have realized that 2 x 2 x 2 x 4 x 7 = 112, because that was the original number that it came from, and the only “additional” factor from 80 is the 5, so you need only multiply by 112 by 5. This then made me realize that if you figure out the greatest common factor, divide one number by that, you can take the quotient (the “extra factor”) and multiply the other original number by it. In this case, if you figure out that the common factor is 16 and then divide 80 by that (maybe halve, halve, halve, and halve? to get 5) then you just need to multiply the other original number (112) by that 5 to get the LCM of 560.

This made me think about something that I don’t think has been mentioned as much in the work of Cathy Fosnot’s “Landscape of Learning” & the work that Pam Harris is doing with secondary strategies. The landscapes always include strategies, models, and big ideas – and Pam has a great blog post distinguishing the difference between strategies and models. But I think models (“representation of a strategy”) doesn’t quite cover everything else, so I almost think there’s ALSO “organizing techniques” (Maybe this is a subset of models?).

Let’s consider the strategy from the video above, sometimes called the grid method, sometimes called the cake method or the ladder method. Essentially, the actual strategy says:

• To find the GCF or LCM of two numbers, divide both numbers by the same factor.
• Then take the quotients and divide by a new common factor.
• Stop when you get to two quotients that are relatively prime.
• The GCF is the product of all of the common divisors (factors) that went into both numbers.
• The LCM is the product of the two quotients that were relatively prime and the GCF.

The model (organization technique?) most people use to represent this strategy is a grid that looks similar to a ladder, a cake, or an upside down division bracket. People have extended the Ladder Method to also apply it to factoring and using the distributive property, even with variables. (Now that I started calling it an organization technique, I’m wondering if it really is just a “model” – but not a model that can be used for other strategies? Or can it??).

Viewing this grid as a table made me think of some work from the CMP3 PD I led on Friday. We were looking at investigation 4.2, and considering the changing dimensions of two adjacent rectangles with a shared side.

If you look at each row, they can easily make an equivalent expression which represents the sums of the two areas (36su + 48su):

• 1(36 + 48)
• 2(18 + 24)
• 3(12 + 16)
• 4(9 + 12)
• 6(6 + 8)
• 12 (3 + 4)

If you notice, the last row shows the greatest common factor on the outside, and the two numbers inside ( ) are relatively prime (3 and 4 share no common factor other than 1). This table could be seen as similar to the grid method, in that each time, the two numbers inside the parentheses were divided by the same factor. The main difference here though is that each row of the table “stands alone” because the factor outside the parentheses kept changing “in real time” and one subsequent row didn’t necessarily follow from the row right before it (i.e. you probably didn’t change the 2(18 + 24) into the 3(12 + 16) >> instead, you probably went back to the original and restarted with a different common factor). Regardless of which factor(s) you found first, you will still end in the same place with the greatest common factor being the 12 that gets pulled out.

I’m not 100% sure yet how this table integrates into the methods for finding the LCM/GCF of two numbers, but it FELT related (though, obviously, it builds on the finding of the GCF, because this is how you “factor” an expression!).

So this whole time, I’ve been feeling weird about the fact that in CMP3, you START with the LCM, and THEN find the GCF… but, in thinking about methods for finding the LCM, you always need to already know the GCF, or else you might just be finding a COMMON MULTIPLE, and not the one that is LEAST. When I went to Illustrative Mathematics’ open up curriculum, they reordered it, so that you find GCF first and THEN LCM! They then separate out the skill of actually USING LCM & GCF to a third lesson.

Of course, in those lessons, it doesn’t teach any particular organization strategy. Mostly, IM expects students to list factors and multiples (probably based on their prior knowledge) and then to circle the common factors or multiples and look for the greatest/least ones. Which (now) leaves me wondering if that’s actually supporting students in growing their thinking strategies, or if it just leaves them stuck in additive thinking strategies when they should be progressing to multiplicative thinking strategies.

I think if I were to classify the different techniques:

• the listing multiples and circling common multiples is probably an additive strategy
• the listing factors and circling common factors could be either an additive or multiplicative strategy, depending on how students obtain the factor list
• Finding the prime factorization (either through factor trees or the grid method, two different models) & then using some model to find the common factors or the common multiples (venn diagrams or the grid) seem to be multiplicative strategies (since they use division)

I think that students in middle school should be moving towards mostly multiplicative thinking, as that’s the necessary groundwork for proportional reasoning, which we need to start this year. So that would make me lean towards finding a good model to represent the division-related strategies, rather than pushing my students towards listing (which is the “previous level’s” thinking). However, I also wonder about imposing a particular organization technique on my students – because let’s be honest, that’s REALLY what the grid method is about. It’s a way to organize your division attempts to collect the factors you’ve found.

Which leads me to why this week’s lessons are still feeling “up in the air.” I don’t think I have made a decision about (a) the order that I’m going to teach GCF/LCM in, or (b) the techniques for finding the GCF/LCM that I’m going to teach. I also need to get all of my classes “caught up” on the number strings from last week – some of the classes got through 4 strings, and some of them only got up to one or two of the strings! I want to make sure all of the students get all of those strings, because I think they develop important strategies in the strings (that will ultimately help us in finding common factors and multiples as well!).

Breaking it down: How do we address student attrition? By analyzing systems that disenfranchise students experiencing trauma #TMCNYC18

I should preface this post by saying that I’ve been thinking a lot about what Sara Van Der Werf calls the Subaru Effect: “One day you go and buy a new car.  You decide to buy a Subaru for the first time.  The next week as you are driving your new Subaru around town you see Subaru’s everywhere you go.  You wonder why you are seeing so many Subaru’s when you would have sworn last week there were very few Subaru’s on the road.  The ‘Subaru Effect’ is your brain being awoken to seeing something around you that was always there, but you just had never paid attention to it before.” In her post, she mentions how once white privilege was given a name, she started noticing what had previously been invisible to her. I have felt similarly, especially since I expanded my twitter PLN over the last year to include far more teachers of color and writers of color who shape my perspective and help me to notice the inequities and underlying structures and systems that reinforce and codify those inequities. So this post below about my experience today at TMC NYC was my most recent “subaru effect” observation, but one that I think is vital we teachers begin to address better.

The first session I attended at TMCNYC on day 2 really made me think about the ways in which we, well-meaning teachers (often white, but not always) refuse to examine the structural causes of disenfranchisement and instead, perform “tokenized” “culturally responsive teaching.” The name of the class was “ Cultural Responsiveness in Math: A Student Research Project” and I attended with the hopes of learning some ideas about how to use a project to make my class more responsive to my students. (The link above goes to a blog post about essentially the same session, but at a different presentation; that author has given a good synopsis of the class, but is not the focus of my blog post on the topic).

To start, Ramon put up the following “problem” on the board to launch his presentation:

“Teaching Problem: For three consecutive semesters, an adult education teacher began classes with roughly 36 students and ended with roughly 12 students. What can the teacher try that will help to reduce attrition?”

Now, he works with adults in a CUNY program that sounds like it tries to help people who’ve been out of school and are now adults get their GEDs/high school equivalencies, and perhaps even prepares them for community college classes.

On the other board, he shared out some of the things he learned from his students about what’s going on in their lives. I’ll summarize, since I didn’t take a photo:

• one student’s twin died, and now this person had to take care of their sister’s three children
• Another person was suicidal
• Another person was living in a shelter
• Another person was a single parent of 6 children and struggling to get by
• one person had lost something like 6 people in their life in the last year

I don’t recall the exact nature of all the statements on the board, but I think you get the gist – these are all real life challenges that adult students in his program were struggling with in terms of coming to class, in terms of being prepared, in terms of passing his classes. And our first discussion was to think about ways we could design a class to reduce the attrition rate, given these challenges.

And at my table, Nancy, Kristen and I (and someone else, I think?) discussed some of the ways to keep students who were having trouble attending engaged in a class. We discussed how if (in a semester of “remedial math”) each class is essential, then if a student misses one or two classes, it may feel hopeless to catch up, whereas if the topics cycle throughout the semester, and students know them in advance, then they can figure out how to make up material they’ve missed. We discussed how that involves pre-planning in advance, but didn’t get into specifics of how to do it in a way that would still make ALL classes relevant to people who were able to attend every class (which, I fully believe is possible, but is NOT the focus of this post, so I’ll save that idea for a future discussion). We also came up with some other ideas that I recorded in my google doc:

• Figure out why students are absent and ask them what you can do to bring them back, perhaps connecting them with college equivalents of guidance counselors or other mental health professionals.
• Normalizing problems – people have a lives outside of class, things come up, life happens, emergencies/urgencies happen, and you need to set your goals and think about how to access the materials and problems when you’re unable to make class so that you can keep up with the instruction. (thinking about using google classroom or moodle or whatever online college system they have as one way to share the problem sets, the lectures/notes, the slides, etc.).
• Potentially starting classes with the same reflection each week, especially focused on re-engaging students who missed the previous class or two, asking “What was the last class you attended? What’s been going on? Why did you come back?”
• We had a question that went unanswered, but I think would also have helped inform our discussion: “How many of the students who drop out in a given semester from this class ultimately drop out from the college as a whole vs. return in a future semester?” Understanding whether the “drop out” is temporary or permanent might help figure out the obstacles that are keeping these students from engaging in the class.

(I didn’t even get a chance to talk about my bigger idea that if

Now, when Ramon called us to share out, Nancy shared the idea about meticulously planning the calendar to support students who’d missed a class in being able to cycle through the topics and revisit the ideas so that it didn’t feel like an impossible task to catch up.

Ramon’s response was to shut down this avenue of thinking. First, he said that there was a pretty strict policy about three absences = an F in the class (though he later recanted and said that he knew that policy wasn’t always strictly enforced in the college in all of the classes, just maybe in this class? it was unclear to me). And he said that one of his goals was to teach his students to BE students – part of that meaning showing up to class, being prepared, bringing their binders (even though they might not want to appear like students). At this point, he said that these skills were important for both college and jobs – not acknowledging at this point that it sounds like some of his adult students might actually BE employed and have jobs – and that might be part of the conflict for some of them!

I jumped in at this point to try to highlight the fact that coping with real life is sometimes quite challenging, and that he wasn’t acknowledging the role that was playing in the student’s “choice” to not attend class (as he framed it). I pointed out that when my uncle died, I was able to take a day off from work to attend his funeral – why wouldn’t it be reasonable to assume a student might need to miss a class or two to deal with taking care of real life issues.

He acknowledged at this point that some part of the absences were due to legitimate issues that are “out of his control” – but then he said “these issues come up more frequently for this population of students” [than the people in this room] (who were mostly white educators vs his students, who he described as primarily Latinx).

And this brings me to my biggest issue and why I wasn’t really engaged with the rest of the presentation:

It felt like he was refusing to acknowledge that this system is set up to disenfranchise students who are experiencing or who have experienced trauma and was refusing to interrogate the structural policies that might be keeping students from passing his class (and thus explain the attrition rate – because if you know you’re going to fail anyway, why would you keep attending?). I don’t know how many times his class meets in a semester (I will start with that acknowledgement), but I personally think any policy that is so numerical and removed from the PEOPLE (i.e. “three absences = F”) is one that is going to reinforce the status quo of inequity because it doesn’t take people’s real lives into consideration. I would much rather have a policy that says something like, “I understand you all have lives outside of school, and I encourage you to contact me as soon as you know of an issue that may conflict with your ability to be here in person so we can work out the details of keeping you up to date and in good status.” and then personalizing your response to each of the students’ individual situations (36 students is NOT that big a number). You can make the judgement call then with the students whether the fact that this person missed two major classes because they were at their child’s parent teacher conference, discussing their child’s class struggles should be enough to fail them, or if that’s a reasonable conflict and you can work with them to create a plan to get caught up.

I would also argue that there was some racism at play here, with the implication that “these issues come up more frequently for this population,” but not acknowledging WHY his student population might be MORE LIKELY to experience trauma in comparison with white educators (I would estimate everyone in that room today had at least a bachelors and probably one masters degree if not more higher education). I’m going to compare some of the situations mentioned on the board to my own life, acknowledging that I’m a relatively privileged white trans man.

First, after two years of college, I decided to take a year off to figure out where I was going to transfer because I didn’t want to be an engineer anymore. During that year, I worked at Space Camp in Huntsville, AL, for both summers. I also went down there to work in January of 2006. However, the Sunday after I graduated from training, I got a phone call from my mom that my dad had died from a heart attack. This news was unexpected and devastating. I immediately spoke to my boss and told her I had to fly home to New York to attend the funeral. Despite the fact that I was originally scheduled to work that week, my boss told me to go and take as long as I needed and to not worry about it. When I got home, my mom asked me to move home for a bit and help her after a hip replacement surgery scheduled for a few months later. So I emailed my boss and explained the situation, and asked if I could quit now and return in late May/early June for the summer session. My boss was flexible and agreed. Now, keep in mind – when I worked in Huntsville, I had to move down there. I was able to live on the campus of Space Camp, but now I was occupying a room there that I wasn’t planning to keep. My bosses let me keep my room until the following month when I was able to fly down, pack everything up, and have a friend with a pick-up truck drive me and my stuff back to New York!

Why do I bring up this story? Because I was coping with the loss of a parent, it impacted my job, and yet – I was able to return to working at Space Camp that summer – my bosses held a space for me. If I had needed to keep working, they would have allowed me to return in one, or two, or three weeks – or whenever I was able to return. Yes, the structure of the camp allowed them the flexibility to have space for me to return, but many jobs (especially at larger companies) do have this flexibility. So merely being absent “three days” was not cause for dismissal from my job!

Second story from my life: In grad school at Sarah Lawrence College, while getting my Master’s in Child Development, I got the flu the week before my thesis was due. While much of my thesis was written, I wound up flat on my back for a whole week and a half. My mom even paid for a cab to take me home to Queens so she could take care of me and I wouldn’t be alone in my apartment! This wound up meaning I missed the deadline to graduate officially in May because I hadn’t submitted my thesis in time. However, my professor gave me an extension until the deadline for the August graduation, and I was still allowed to walk at graduation and participate in the graduation ceremony – my diploma just didn’t get mailed to me until August when I “officially” graduated. I obviously missed my classes that week, including my field work at the Early Childhood Center (who in fact said “don’t bring the flu to our young children!), but again, was not penalized for missing class – just had the expectation that I would catch up on the material I missed (and probably was discussed in my conferences with each professor).

Yet again, I experienced a (more minor) trauma – a serious illness that kicked my butt for almost two weeks at a critical moment in the semester. However, I didn’t fail any of my classes, and despite missing my deadline to submit my masters thesis, I still got my degree! And now? Ten years later? No one cares whether my diploma was awarded in May or in August or the reason behind it!

I could go on, naming multiple other experiences where I’ve experienced a problem in my life (family member’s death, a hospitalization, an illness, etc.) where the boss or professor to whom I was accountable was understanding of my situation and able to work with me to accommodate my needs, support me while I was recovering/grieving/etc., and then to help me catch up once I was better. Now, I need to acknowledge that being raised by my mom, I was taught to advocate for myself, to reach out to professors in advance whenever possible, etc. Those are LIFE SKILLS and STUDENT SKILLS that are necessary for people to know how to “work the system” and get the support they needed – and yet, I would bet that these are skills that Ramon’s students might not all have mastered. Why isn’t this self-advocacy skill one that he’s willing or interesting to teach them, rather than the static “they have to be in class with a minimum of absences”?

Plus, Nancy pointed out that the skill to manage time is another executive functioning skill that people need in the “real world” of college and work. Thinking about how to schedule your time so that you have enough time to do your HW or accomplish projects for work, even while making your “social life” plans or balancing your children/family’s needs with your school needs are an important work/life balance skill that many of us struggle with – me included. And here again, there’s an opportunity to talk about how to set up routine in one’s schedule to try to have the time to accomplish the HW, and estimating how much time it will take outside of class, and figuring out a back-up time of how to get caught up if something comes up with the first time. But again, this was a skill that he wasn’t interested in talking about.

Instead, Ramon then shifted into his “main point” about cultural responsiveness, where he laid out the situation as follows:

“problem: severe attrition, potentially due to student cultures not being acknowledged, recognized, or incorporated enough,”

So his possible solution was to recognize student’s cultural values, as this might motivate students who were “teetering” on the decision of whether to attend to choose to attend his class, despite the issues coming up in their lives.

Thus, he planned and executed a project with the students, where they chose a “cultural artifact” and researched the math behind it, then writing a poem, or writing a math problem, or producing some other kind of written product about it. In flipping through the book he’d made of his student work, some of them wrote poems, some of them wrote problems, and one of them analyzed a game called Skellzies which we had an opportunity to play.

However, I felt like this was a superficial bridge between people’s selves and their schooling, hence my use of the word “tokenization” in my opening. Student cultures were “incorporated” in a research project that wasn’t directly tied to the math they had to learn for the class, and it isn’t addressing the underlying structural policies that are perpetuating the attrition issue in the first place. It seems disingenuous to try to “incorporate student cultures” to make the class more “responsive to them” when it’s not also supporting them in accessing the class itself.

Now, I should note here: I don’t have an issue with the IDEA of incorporating research projects that encourage students to connect math to their identities so they can see themselves as mathematicians – in fact, I think we need to do much more in our classrooms, in general, to posit students, especially oppressed groups, to see themselves as mathematicians, but I think BOTH avenues are necessary. I confess I haven’t done enough research into trauma-informed educational practices, but it seems to me that the attrition rate might be further reduced by addressing the trauma students are experiencing differently. A quick google search leads to this link about how to maintain school engagement in students experiencing trauma. I don’t think it’s enough to merely state that incorporating student cultures into math class will keep them from dropping out. Rather, I think that’s one of two (or more) major components – the other is an analysis of the systems, policies, and procedures in place that act as gatekeepers, potentially preventing students from succeeding.

NYC’s mini Twitter Math Camp #TMCNYC18

Have you seen the schedule for TMC NYC yet?

https://tmcnyc.wordpress.com/2018-sessions/

I’m facilitating twice about two different topics. Each day has a theme, so on the first day, I’m going to be leading a session about the distributive property through the grades. I had a brainstorm about it because of my work with the Illustrative Mathematics curriculum this year, but I’m kind of excited to explore this topic with other math teachers.

On the second day, I’ll be evangelizing about one of my favorite teaching techniques: an instructional routine called Connecting Representations, created by the fabulous Grace Kelemanik and Amy Lucenta. You can read more about it in their book, Routines for Reasoning or check out their website, fosteringmathpractices.com, if you can’t attend my session.

I was probably one of the hardest converts initially, the most resistant to actually trying out the routines in my room, for fear that I would get it wrong – and now I’m a true believer and planning to launch my year with three CthenCs (a different routine for reasoning).

Anyway, there’s tons of other awesome sessions to check out, and the best part? The conference is free! (And local, so if you’re in NYC anyway, there’s no need to pay for lodging or more transportation than your typical metrocard!). Registration closes on August 20th, so get in now, before it’s too late!

#ClearTheAir Troublemakers Week #1-2

I couldn’t join the live chats for the #CleartheAir Troublemakers weeks 1 or 2. It’s probably for the best, as I don’t do great with twitter chats (I’m still figuring out how to follow them on tweetdeck), but also because I haven’t had a chance to read the book yet. However, the organizer, Val Brown, posted the questions in a twitter moment, so I decided to copy them here, and respond to them as a blog post. Which, for my loquacious self, is probably for the best, given how many words I’ll need (main reason I was resistant to twitter for so long – what can you even say in 140 characters??)

#ClearTheAir QHQ #1 – Preface:

“Our children bear witness to an unimaginable array of examples of throwaway lives…” and “our children are learning that only some lives matter…” 1/2

— Val Brown (@ValeriaBrownEdu) August 1, 2018

Define indifference, and share some of the ways you have communicated indifference or that only some lives matter to your students? Consider why you do (or have done) that and share with us. What are you going to do differently this year?#ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 1, 2018

Indifference is a lack of interest, concern, or sympathy, according to the dictionary. What it may look like in my classroom is not asking students about themselves enough – do I have an interest in who they are as a person? Or do I only have interest and assign value to them as a student (in particular, as a math student)?

I think I’ve been doing a better job over my 8 years, of shifting from my view that the content was the key to figuring out how to balance interest in my students and their lives (all of them!) by taking a moment to talk to them and ask them about themselves or chat with them. I know the last two years, using the name tents, has helped me to get to know my students better and learn about their lives – but I still could be doing better.

I think one goal I’m going to try for this year is tracking which students I’ve spoken to “socially” (either in the hallway, or after school, or before/after class, or even during a break), and try to ensure that I’m equitable about my attention, ensuring that I check in with everyone at least once a month or so. Maybe I can use my attendance/seating chart to check off when I’ve spoken with a kid in a given week/month, and if I notice there are no checks next to a name, I can be sure to talk to them next.

I also know that as someone with ADHD, I often struggle to focus or listen to other people. I’m a big interrupter and I often center myself in conversations. Decentering myself and asking about the other person (and truly listening to understand, not just waiting my turn) is a skill that I’m still working on developing. And this question makes me think that cultivating that skill in my classroom is important (as well as in my personal life), so I’m going to try to be more intentional about listening to understand my students. (And knowing my strength as a writer/reader, I wonder if I can somehow re-use the idea of the name tents later in the year, to continue a conversation with my students – maybe we can do it on index cards or something – have a “silent” conversation).

#ClearTheAir QHQ #2 – On (In)Visibility
“Thus, the withholding of education is a political tool used to maintain and ensure an economic and social underclass…In this way, schools are deeply implicated in the systematic maintenance of the racialized American caste system.”

— Val Brown (@ValeriaBrownEdu) August 1, 2018

What is the connection between your classroom and the maintenance of the racialized American caste system? If your classroom wasn’t implicated (because we know it is) in the systematic maintenance of the racialized American caste system, what would it look like? #ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 1, 2018

Well, just thinking about who’s actually IN my classroom at the various schools I’ve been at shows the most direct connection. For example, my first school in the Bronx had NO white students, few Asian students, and mostly Latinx and black students, so that was who I taught. My second school on the Upper East Side had a big mixture – except that in the honors classes (not mine) were the mostly white and Asian students, so my classes had a wider variety. However, the academic (or “low level”) class had more black and Latinx students than my other classes, solidifying the tracking by race (even if not consciously doing so).

Envisioning what my classroom would look like if it were free from that is hard because every time I think I understand the racism in this country, I uncover yet another aspect that I was previously blind to. I think ultimately, if it weren’t implicated, every school’s demographic make-up would match the city’s demographic make-up. Every class would be of equal quality for ALL of the students in it. All students would be empowered to advocate for themselves and each other. Beyond that, I’m not sure yet. Clearly, this is something I’ve got more reflection to do (maybe I’ll hunt down the twitter chat and read other people’s responses to this question – I’m not sure how to do that yet).

#ClearTheAir QHQ3 – Zora

The Ts wanted Zora and Lucas to fit into classroom that matched the cultural expectations “of an overwhelmingly white, mainstream majority.” Zora’s parents (POC) initially resisted and Lucas’s mom (a white woman) wanted compliance as soon as possible.

— Val Brown (@ValeriaBrownEdu) August 2, 2018

How are white values interpreted as American values? How do white values hold everyone hostage?#ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 2, 2018

White values are assumed by many white people to be universal, probably in part because so much of “white culture” is reflected in American Television as “universal.” We see the same expectations reflected in so many places, we begin to think they really are ubiquitous without recognizing that it’s a cultural value, and that other cultures may have other values, but are not deficient merely because they don’t value the exact same qualities white culture does.

I keep thinking about the difference between white church and black church and the analogy someone made between white and black student participation in classes (was that on twitter? In a blog? A conversation in person? I can’t remember now). My first year teaching, I responded so horribly every time a kid called out an answer. I would shut them down, and tell them that’s not how to participate in class. I often would have one-way conversations with the class, reminding them that to participate, we needed to raise our hands – because that’s what I’d been taught at my predominantly white teachers college.  Whereas this most recent year, when one of my enthusiastic black girls would call out, I would often cheer her on and direct attention to her contribution. Sometimes, I had private conversations with her to remind her that I wanted to give other people a chance to participate also, but I was excited by her enthusiasm. I think in that response, I was better able to convey to her WHY it was important some times not to call out (because I value think time and hearing a variety of voices), rather than just silencing her. I think the white value of “docile and quiet” held me hostage my first year teaching, because I didn’t recognize the ways students were acting was based on a different cultural value – just one I wasn’t tuned in to see.

The last school that I worked at was predominantly white and Asian, and many of the teachers would complain about a lack of participation by the “quiet Asian students.” I’m now re-viewing those moments through this lens of white cultural expectations, and I wonder if the white value that everyone is extroverted and verbal ignores different cultural values from my Chinese students’ backgrounds. This seed was planted when I read the book, Quiet, but I still haven’t quite figured out how to integrate this new recognition with my actual teaching practice. I’m thinking about how to ensure all student voices are heard even from students who are quiet, and I’m still wondering about ways to get their voices “heard” through written responses that get shared (anonymously?).

#ClearTheAir QHQ4 – Lucas

“…who the hell wants to imitate life? Here’s a chance to make magic and you’re going out imitating life. That just seemed like a waste.” Mo Willems

— Val Brown (@ValeriaBrownEdu) August 2, 2018

What would you have to change (personally or professionally) in order for your class or school to stop perpetuating the status quo and instead be a place where Ss can imagine freedom, practice freedom, and prepare for freedom?#ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 2, 2018

How do we stop perpetuating the status quo? That’s a tough one; I feel like I’m still figuring out what the status quo is because so much of it is invisible “universal expectations” that I’m finally becoming more and more aware of.

I have a confession to make: sometimes, when I think about how to practice academic freedom, I don’t know how to do it as a MATH teacher. I can envision it as a humanities teacher (man, the things my students and I would read and write! I’m so inspired by all of the humanities teachers I see doing wonderful and empowering things!).

I’m still reflecting on how I would need to change my class to imagine mathematical freedom, to practice mathematical freedom, and prepare for mathematical freedom. Some of it, I think, is in empowering my students to think for themselves – which I think I’ve done a pretty good job at over the last few years. I think some of it is about empowering my students to see math as a tool for making sense of their own lives. I also wonder if some of it is about empowering students to ask the questions that we investigate and figuring out how to modify the curriculum so we can explore their ideas more. I’m not sure.

I think one of the biggest things that I need to change immediately is the way I deal with student behavior. I’ve already grown so much from the first year teacher I once was who thought every student’s behavior needed to be corrected with detention by recognizing that most challenging student behavior is communicating unmet needs or lagging skills and it’s my job to help ensure those needs are met and those skills are taught (by me or elsewhere) (this is the model from Ramapo for Children & Dr. Ross Green). So I’m definitely much further along this growth path than I was, but I think I still need to be more intentional about it. The last two years, I’ve been at a school that had minimal behavior problems because it screened students heavily (based on grades and performance on a three-part entrance exam), but at my previous school, I relied on suspensions for especially challenging behaviors (like pushing over desks or “insubordination” along with cursing at me). I’m hoping that my new school’s focus on mindful breathing and circles during advisory will allow me opportunities to learn more about restorative justice practices, and figuring out how to focus more on building the relationships with my students that are vital. I checked out that website (I forget the link) that tracks data on suspensions by race, and my new school as well as the previous two, disproportionately suspend black and latinx students. I want to be more cognizant of that, and interrogate my practices – if I am thinking about how to discipline a child of color, would I interpret their same behaviors differently if a white student were doing it?

I’m also thinking about this post by Jess. In particular, I’m struck by this quote, “We are raising our students to put compliance above justice, to follow blindly without asking if what they are following is fair or just. We are raising the humans that perpetuate these conditions. But we do not have to. We can change that narrative. We can start to use our students’ noncompliance, not as a reason to punish, but as an opportunity to learn. To learn what we need to fix.” I’m wondering how I can have a similar conversation with my students about the rules. (As a MS math teacher, with three classes, and a more limited amount of time for each class, I always question how I can devote time to conversations like these that seem “out of place” – but then, as a disruptor, I question how I can avoid having these important conversations with them!)

QHQ#1: The Crossroads School
Ageism has been generally defined as a prejudice people from a certain age group toward other age groups. #ClearTheAir 1/

— Val Brown (@ValeriaBrownEdu) August 8, 2018

How does ageism impact classroom rules, procedures, and management systems? How are your rules/procedures an expression of what you think about young people, their agency, and their place in your classroom? #ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 8, 2018

In most classrooms, the rules, procedures, etc. are formed by the teacher… often before the students even arrive! So in many ways, I think ageism impacts class rules, procedures, etc. because we assume the adults can (and SHOULD) make all of those with minimal input from the students – and even when we solicit student input, they usually come up with the same general ideas – often regurgitated from last year’s teacher’s rules!

I often feel stuck about this topic of including students in doing more/creating more responsibility for them (probably in part because I’m nervous about giving up control to my students, and partially because I’m bad at improv!). I think I’m of two minds when it comes to student agency: I want them to be empowered to be agents of their own learning, but when we’re in our classroom community, I also want them to be a member of our community… But I know that some of the expectations I have for math class (as a constructivist teacher) are different than what they’re “used to” – so I don’t know how to balance my experience and knowledge about how to best make sense of math vs some of their desire to just “be told what to do.” Maybe some of the answer lies in having a conversation with students about how learning works and getting them to buy into constructivism in order to turn over more agency to them?

Otherwise, in terms of rules and procedures, I feel like I basically have one big rule at this point: our goal is to do math and think like mathematicians for the entire time we’re together, and anything that distracts from that needs to be set aside and saved for another time. I do use hand signals for the bathroom in part because I want to make sure that students are not going when I’m about to say something super important (unless it’s an emergency), and also because most of the schools I’ve worked at have required teacher signatures on bathroom passes of some kind. I try to take myself out of the process as much as possible, though, teaching kids the non-verbal ways I’ll respond to them so they can go. As for getting pencils or other supplies, I have cards on the desks, and I’ll usually call out a suit to go do something, “All of the hearts, go get rulers for your group” or whatever they may need.

I definitely need to reflect more about this one, though. I don’t think I’m doing a good enough job at it yet.

QHQ#2: Sean –
For Sean, disruption plays an important role – social connection, affirmation, negative attention. Now understanding that Sean wants to be seen, we may be able to better empathize with him. 1/n

— Val Brown (@ValeriaBrownEdu) August 8, 2018

Martin Luther King, Jr. said, “A riot is the language of the unheard, and what is it that America has failed to hear?” 2/n #ClearTheAir https://t.co/gQt1EyTvWE

— Val Brown (@ValeriaBrownEdu) August 8, 2018

Make some connections between Sean’s story and how we view civil disobedience (say…Colin Kaepernick kneeling during the anthem, BLM protests). How have you viewed those movements or talked about those movements? What is your thinking now? #ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 8, 2018

I’m definitely seeing a connection between the snippet of Sean I’m getting here and the civil disobedience movements – people who are not a part of them often react negatively to them and want to squelch them (such as the NFL’s new rules about standing or the all/blue lives matter response). I see that as the teacher who wants a student like Sean to become compliant and to “fall in line.”

However, now I’m thinking about those movements as drawing attention to something that has been ignored or gone unheard by the general populace – such as police brutality and the connection to student disruption. I wonder if we can expand viewing the challenging behavior as communicating unmet needs and lagging skills to viewing riots as the ultimate communicate of unmet needs and lagging skills.

QHQ#3 – Marcus and Sean are both excluded when they don’t meet the T expectations. Complete any of the following sentence frames (or make up your own) and then expand on your answer. 1/2 #ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 9, 2018

Sentence frames –
I learned the practice of exclusion …
Practicing exclusion communicates and teaches … to students
Last year I used the practice of exclusion and now I am thinking…#ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 9, 2018

I first learned the practice of exclusion as a student. I was excluded by my teacher in first grade, and later by my peers in middle school and high school. The exclusion taught me that I was unwelcome, that there was something wrong with me, that I didn’t belong. It didn’t meet any of my needs, and it honestly didn’t change any of the things about me that made those people exclude me. It wasn’t until I was an adult, and in a community where I felt accepted for me, that I was able to share my stories of exclusion with people who helped me to make sense of the behaviors that I might have been doing that caused others to exclude me. So, ironically, it was through inclusion in another community, that I learned how to mature and evolve, not through the exclusion from my initial community. I now recognize that some of my exclusion was due to my social awkwardness (a side effect of my ADHD and the way I used verbal communication – talking fast and about me/my ideas, interrupting others, not listening to their ideas) and some of it was due to being queer and trans at a time when my peers and parents didn’t have that language and I felt misunderstood.

As a teacher, I think about exclusions as class removals/suspensions (where we’re excluding students from the learning experience in our classroom communities) and being prohibited from going on a field trip. The longer I’ve been a teacher and the more experienced I’ve become, the more I try to limit my use of exclusion, as I’m recognizing that it merely removes a student from the situation, but it doesn’t actually make anything better in and of itself. I’ve already thought about restorative justice as the next thing I need to learn about and become proficient in, but now, making the connection between my own feelings of exclusion as a kid, and knowing what little I do know about RJ, I think it’s the way to combat the isolation that is felt by someone who is being excluded, and instead, to rebuild the connection to the community, so that more positive behavior will happen.

QHQ#4 – Zora, Lucas, Sean, and Marcus all wanted the same thing – to be able to be themselves. #ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 9, 2018

Talk about a time you were able to be “fully human” with someone. What were the conditions that made that possible? How did it feel? What can we do to replicate those conditions in our classrooms? #ClearTheAir

— Val Brown (@ValeriaBrownEdu) August 9, 2018

I’m not even 100% sure what being “fully human” is because I feel like it probably happens so rarely. As with any human, I am multi-faceted, but some of the aspects of myself have communities that seem to be incongruous or incompatible with each other. For example, I am ever cognizant of how being an openly sexual human makes some people (especially religious people) uncomfortable. Plus, several branches of Christianity think because I’m queer (and have sex outside of marriage) and/or because I’m trans (and I used medical science to change my body to alleviate my dysphoria), I’m a horrible sinner and I’m going to hell or what have you. Because I’m aware of the overlap between my teacher circle (where I can be fully a teacher and talk about edu) and religious folks (I notice Christ or Jesus in the profiles of MANY of the people I follow on twitter or my followers), I’m often uncomfortable and hold back. I don’t know how those people feel about me – if they’re going to judge me for my trans-ness or my queer-ness, or the fact that I’m anti-assimilationist (i.e. I’m not exactly like you cisgender, heteronormative, monogamous, religious folks and I don’t want to live my life according to YOUR values), it makes me uncomfortable to be myself around them (and even here, typing these words into my blog, I’m carefully considering how to phrase everything just right so that I don’t offend or alienate someone unintentionally).

On the other hand, I think about my tiny queer/trans circle of fellow educators – both the NYC community at large and the MfA community that I’ve been cultivating over the last year, and I think about how much easier it is to be authentic with those folks because I know they’re less likely to judge me for my transness or my sexuality.  But simultaneously, I also know that I can be fully my educator self, because they understand those aspects of me too.

I also think about my tight circle of friends (I have two romantic partners and a few really close friends), where I know I can be myself and I will be accepted. I won’t be judged, though I might be challenged or corrected. It will be done from a place of care and loving, with the goal/intention of helping me improve myself – not with the intention of “putting me in my place.” Some of it, honestly, is because I know that most of these people either have these “traits” in common (i.e. they’re also queer and/or trans) or I know their views about them to be positive and affirming.

I think the key to being fully human is probably knowledge that there’s unconditional acceptance on the other side of the relationship. That no matter if you come out as trans, or queer, or poly, or anything else, that person is going to respect you, love you, care about you in exactly the same way as before (or maybe more).

I’m honestly not sure yet how to replicate that in my classroom. I struggle in general with being authentic and not robotic (and not just with my students) whenever I’m nervous (and I always get stage fright at the start of the school year!), so I’m still figuring out how to convey my acceptance for my students. And I know that it’s not just enough to be accepting of students who are like me (i.e. queer or trans), but it’s also about making it safe for all students to be vulnerable, even ones who are different from me. So while it’s easy to become the GSA advisor and help create the safe space for the queer/trans students, it’s less straightforward to me about how to do that for ALL students in my MATH class – I think part of it is about being comfortable being vulnerable with the students (modeling how to be vulnerable and how to react to discomfort from being vulnerable) as well as how to value their vulnerableness when they’re willing to share that with me/us.

 

Just to #cleartheair, typing this up and making it public is an act of vulnerability too. But I think part of the purpose of these chats is to be open and reflective so we can improve ourselves. And it can be nerve-wracking to acknowledge that we’re not perfect, that we still do things that are perpetuating the status quo that we so vehemently disagree with, but hopefully, by hitting publish, I’m taking another step in my evolution as a better educator.

 

Thank you to Val Brown for organizing the clear the air chats. I appreciate the space to reflect on myself as an educator and a human.